Un compte Premium offert sur le site FCL.055 ! Rendez-vous sur www.fcl055-exam.fr puis créez un compte avec le même email que celui...   [Lire la suite]


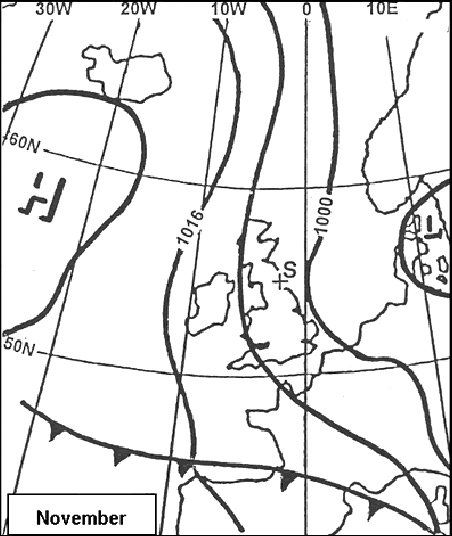
Which aeronautical chart symbol indicates a group of lighted obstacles . 2509 ? [ Formation assignment ]

Question 166-1 : 12 9 10 11

Admin . 2512 exemple 266 12.12.

Which aeronautical chart symbol indicates an exceptionally high unlighted ?

Question 166-2 : 13 11 10 9

Admin . 2512 exemple 270 13.13.

Which aeronautical chart symbol indicates an exceptionally high lighted ?

Question 166-3 : 14 10 12 13

Admin . 2512 exemple 274 14.14.

What is the meaning of aeronautical chart symbol n°15 . 2509 ?

Question 166-4 : Aeronautical ground light visual reference point hazard to aerial navigation lighthouse

Admin . 2512 exemple 278 Aeronautical ground light.Aeronautical ground light.

What is the meaning of aeronautical chart symbol no 16 . 2509 ?

Question 166-5 : Lightship off shore helicopter landing platform shipwreck showing above the surface at low tide off shore lighthouse

Admin . 2512 exemple 282 Lightship.Lightship.

Which aeronautical chart symbol indicates an aeronautical ground light . 2509 ?

Question 166-6 : 15 16 10 14

Admin . 2512 exemple 286 15.15.

Which aeronautical chart symbol indicates a lightship . 2509 ?

Question 166-7 : 16 10 12 14

Admin . 2512 exemple 290 16.16.

Given .a polar stereographic chart of the northern hemisphere whose grid is ?

Question 166-8 : 229° 099° 279° 049°

Admin .let's assume the airplane is at latitude 70°n . 2059.true course = 344° 115° = 229° . ninorr .just remember simple quote . grid track = true track + west longitude or east longitude .so in this case 344 = x + 115.x = 344 115.x = 229 exemple 294 229°.229°.

A straight line is drawn on a lamberts conformal conic chart between two ?

Question 166-9 : Chart convergency earth convergency conversion angle difference in longitude

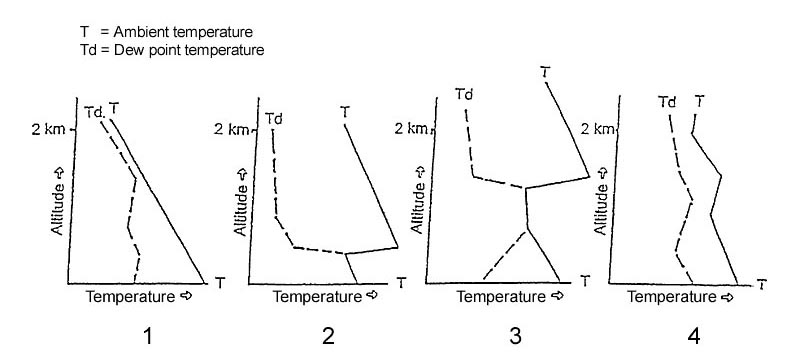Admin .chart convergency means the rate at which meridians drawn on a chart are converging . 2060.if you drawn a line between two positions of different longitude the angular difference between the initial true track and the final true track is equal to chart convergency exemple 298 Chart convergency.Chart convergency.

If the chart scale is 1 500 000 what earth distance would be represented by 7 ?

Question 166-10 : 35 000 m 3 5 km 35 nm 0 35 km

.7 cm x 500 000 cm = 3 500 000 cm = 35 000 m or 35 km exemple 302 35 000 m.35 000 m.

What is the constant of the cone for a lambert conic projection whose standard ?

Question 166-11 : 0 866 0 941 0 5 0 766

Constant of cone convergency factor the ratio between the top angle of the unfolded cone and 360° or sine of the parallel of origin .the parallel of origin is about half way between the standard parallels .midway between 50°n and 70°n is 60°n .sin of 60° = 0 866 exemple 306 0.8660.866

On a direct mercator projection a particular chart length is measured at 30°n ?

Question 166-12 : A smaller distance twice the distance the same distance a larger distance

Admin . 1753. direct mercator chart .earth distance along a parallel of latitude is known as 'departure' .earth distance between two meridians along a parallel of latitude departure = difference of longitude x 60 nm x cos latitude .cos 30 = 0 866.cos 60 = 0 5.if for example the length on the chart is 5° of longitude and measures 10 cm long the distance on earth at 30°n is .distance = 5° x 60 nm x 0 866 = 260 nm .at 60°n and since the direct mercator chart is of rectangular shape 10 cm = 5° of longitude also .distance = 5° x 60 nm x 0 5 = 150 nm exemple 310 A smaller distance.A smaller distance.

How does the scale vary in a direct mercator chart the scale ?

Question 166-13 : Increases with increasing distance from the equator decreases with increasing distance from the equator is constant increases south of the equator and decreases north of the equator

Admin . 1753.on earth 1° of longitude = 60 nm at the equator.at 45°n or s 1° of longitude = 60 nm x cos45° = 42 5 nm.if you look at a direct mercator chart the scale between each degrees of longitude remains unchanged even if you are at 30°n 45°n or 60°n the scale increases with the secant of latitude exemple 314 Increases with increasing distance from the equator.Increases with increasing distance from the equator.

How does the chart convergency change with latitude in a lambert conformal ?

Question 166-14 : It is constant and does not change with latitude it changes with cosine of latitude it increases with increase of latitude it changes with sine of latitude

Admin . 2052.meridians are converging at a constant rate regardless of latitude exemple 318 It is constant and does not change with latitude.It is constant and does not change with latitude.

How does the convergency of any two meridians on the earth change with varying ?

Question 166-15 : It changes as sine of latitude it changes as cosine of latitude it increases with decrease of latitude it is of constant value and does not change with latitude

exemple 322 It changes as sine of latitude.It changes as sine of latitude.

Grid heading is 299° grid convergency is 55° west and magnetic variation is ?

Question 166-16 : 084° 334° 154° 264°

.'convergence east true track least' or 'convergence west true track best' .grid convergency is 55° west .299° + 55° = 354° true track .'variation east magnetic least' or 'variation west magnetic best' .magnetic variation is 90° west .354° + 90° 084° magnetic heading exemple 326 084°.084°.

Where on a direct mercator projection is the chart convergency correct compared ?

Question 166-17 : At the equator at the two parallels of tangency at the poles all over the chart

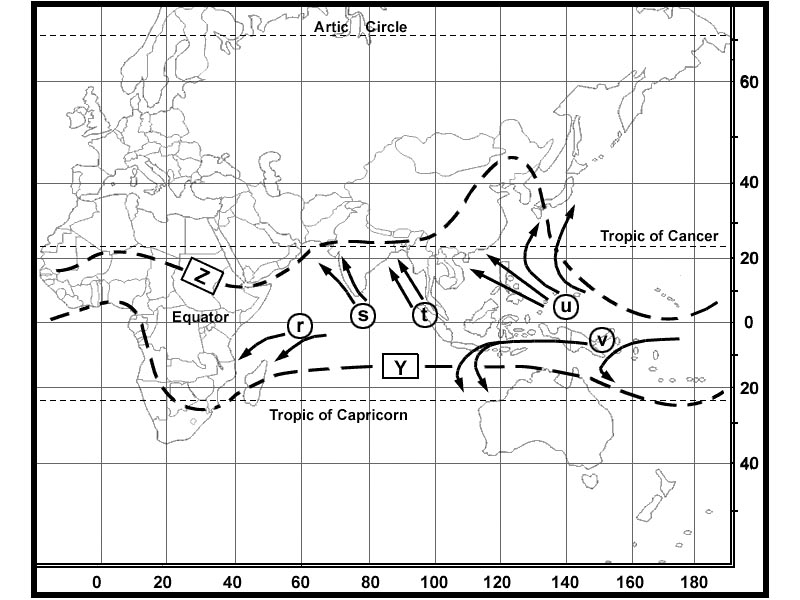Admin .a cylindrical projection based on the equator is a direct mercator projection . 2044.chart convergency = earth convergency at the equator .convergency is the angle of inclination between two selected meridians measured at a given latitude and is equal to the difference between the great circle directions measured at each meridian exemple 330 At the equator.At the equator.

A route a to b is drawn on a polar stereographic chart with the grid aligned ?

Question 166-18 : 350° g 010° g 130° g 060° g

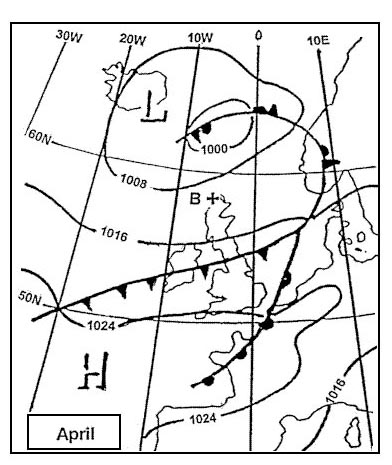Admin .the easiest way to solve this exercice is to draw the situation . 2033 exemple 334 350°(g).350°(g).

The standard parallels of a lambert chart are 26°n and 48°n and the stated ?

Question 166-19 : The scale at 28°n is smaller than the scale at 24°n the scale at 37°n is larger than the scale at 20°n the scale at 46°n is larger than the scale at 50°n the scale at 30°n is smaller than the scale at 37°n

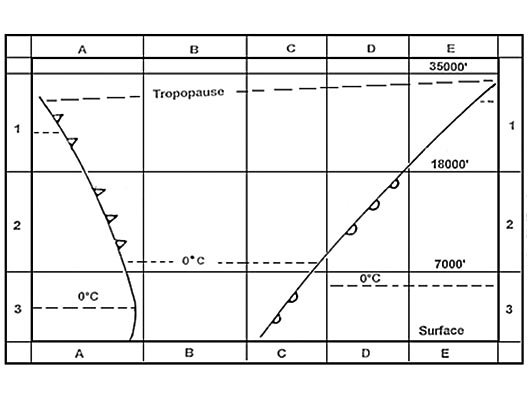.at 26°n and 48°n the stated scale is correct 1 cm = 2 500 000 cm .on a lambert chart the scale contracts between the standard parallels and expands outside so the scale at 28°n is smaller than the scale at 24°n exemple 338 The scale at 28°n is smaller than the scale at 24°n.The scale at 28°n is smaller than the scale at 24°n.

Which statement is correct about the scale of a polar stereographic projection ?

Question 166-20 : The scale reaches its minimum value at the north pole the scale reaches its minimum value at the equator the scale reaches its maximum value at the 45°n the scale reaches its maximum value at the north pole

Admin .on a polar stereographic chart meridians are straight lines originating from the pole parallels of latitude are arcs of circles centred at the pole .the scale is correct at the pole elsewhere it expands as sec² 1/2 co latitude within 1% from latitudes 90° to 78° within 3% from latitudes 78° to 70° exemple 342 The scale reaches its minimum value at the north pole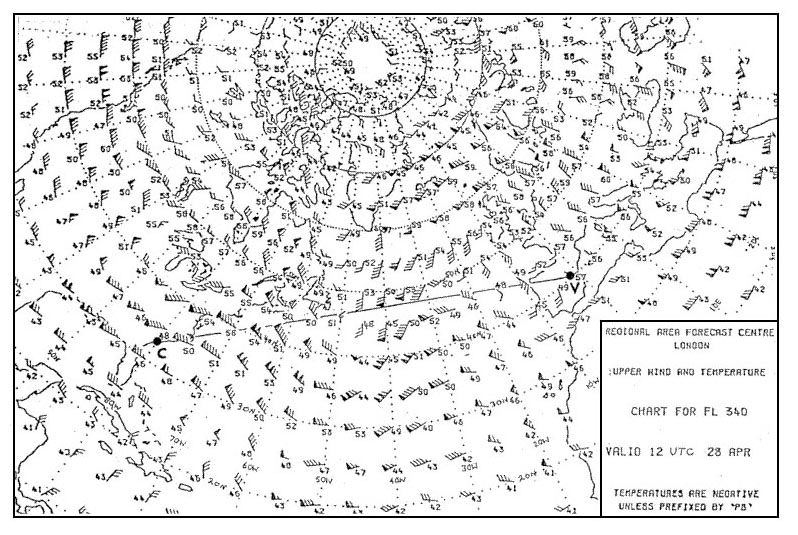.The scale reaches its minimum value at the north pole.

Which statement is correct about the scale of a lambert projection ?

Question 166-21 : The scale reaches its minimum value at the parallel of origin the scale reaches its minimum value at the standard parallels the scale reaches its maximum value at the parallel of origin the scale reaches its maximum value at the standard parallels

Admin .the lambert conformal projection is what most of today's aeronautical charts are based on . 1776.on a lamberts chart scale is correct at the standard parallels as this is where the paper touches the reduced earth and since the surface of the reduced earth is bulging out from the paper between the standard parallels it will have to be squashed in order to fit onto the paper this will then lead to a smaller scale for the area between the standard parallels exemple 346 The scale reaches its minimum value at the parallel of origin.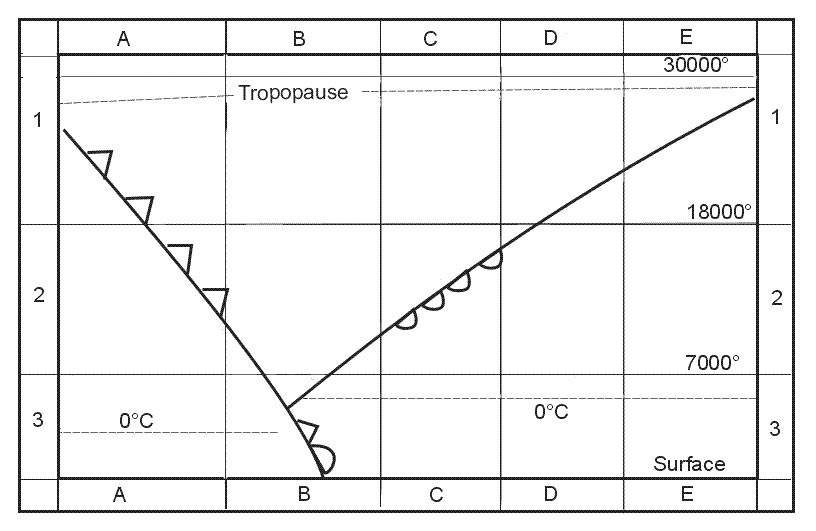The scale reaches its minimum value at the parallel of origin.

A route is flown from 80°s 100°w to 80°s 140°e at 180°e/w the grid track ?

Question 166-22 : 110° g and 290° t 070° g and 250° t 290° g and 110° t 250° g and 070° t

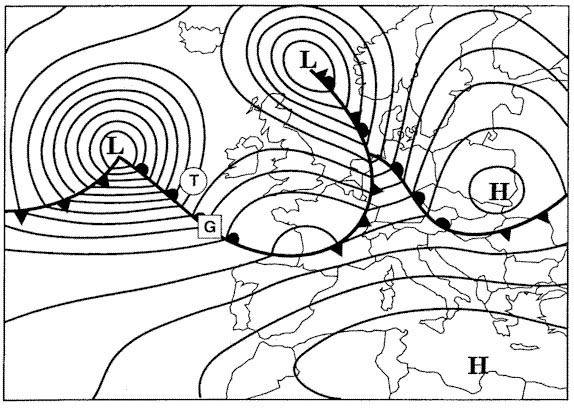.draw the situation . /com en/com061 598 jpg.those questions are not looking your calculation skill but your facility to visualize a situation exemple 350 110°(g) and 290°(t).110°(g) and 290°(t).

A route is flown from 85°s 100°e to 85°s 140°w at 180°e/w the grid track ?

Question 166-23 : 250° g and 070° t 070° g and 250° t 290° g and 110° t 110° g and 290° t

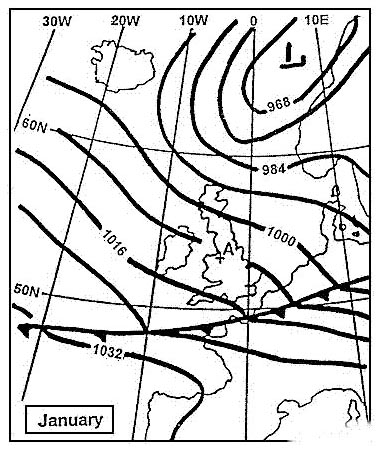.draw the situation . /com en/com061 599 jpg.those questions are not looking your calculation skill but your facility to visualize a situation exemple 354 250°(g) and 070°(t).250°(g) and 070°(t).

The positions a 30°00'n 017°30'e and b at longitude 30°00'n 023°30'e are ?

Question 166-24 : 091 5° 082 5° 085 5° 094 5°

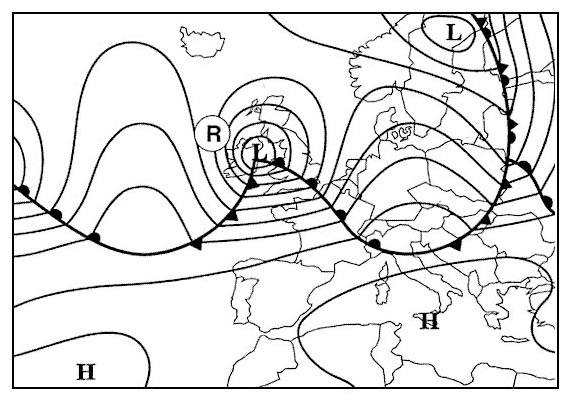.draw the situtation . /com en/com061 601 jpg.if we were on a mercator chart we would have a curve blue line for the great circle track and a straight line for the rhumb line in northern hemisphere our arrival track at b will be more than our departure track at a .simply calculate convergency = 6° x 0 5 = 3°.true track at b = 88 5° + 3° = 91 5° exemple 358 091.5°091.5°

A route is flown from 85°s 100°e to 85°s 140°w at 160°e the grid track gt ?

Question 166-25 : 070° g and 090° t 090° g and 070° t 250° g and 090° t 090° g and 250° t

. /com en/com061 604 jpg. exemple 362 070°(g) and 090°(t).070°(g) and 090°(t).

A straight line from a 75°s 120°e to b 75°s 160°e is drawn on a polar ?

Question 166-26 : 075° 095° 105° 255°

. /com en/com061 607a jpg. /com en/com061 607b jpg.drawn the situation the answer becomes simple and clear exemple 366 075°.075°.

On a mercator's projection the distance between 17°n 035°e and 17°n 040°e ?

Question 166-27 : 1 6 052 030 1 5 556 000 1 10 626 460 1 18 658 470

.on a mercator chart meridians of longitude are parallel lines .5 cm distance at 17°n = 5 cm at 57°n..distance on earth between the two points .distance on earth = change of longitude x cos latitude.distance on earth = 5°x 60' x cos57°.distance on earth = 164 nm ..so we can say that 5 cm on the chart = 164 nm on earth..164 nm x 1 852 = 303 728 km.303 728 km x 1000 = 303 728 m.303 728 m x 100 = 30 72 800 cm..30 72 800 cm / 5 cm = 6 074 560.the scale at 57°n is approximately 1 6 074 560 exemple 370 1 : 6 052 0301 : 6 052 030

A straight line from a 53°s 155°e to b 53°s 170°w is drawn on a lambert ?

Question 166-28 : 078° 102° 282° 258°

.draw the situtation . /com en/com061 616a jpg. /com en/com061 616b jpg.we can go for calculation .change of longitude = 35°.convergency = change longitude x sin latitude.convergency = 35° x sin 53° = 28°.departure track at a is 090° + 28° = 118°.track on arrival at b = 090° 28° = 062° .at half way between a and b track is 090° .175°w is on the last part of the flight so our true track will be less than 090° and more than 062° . 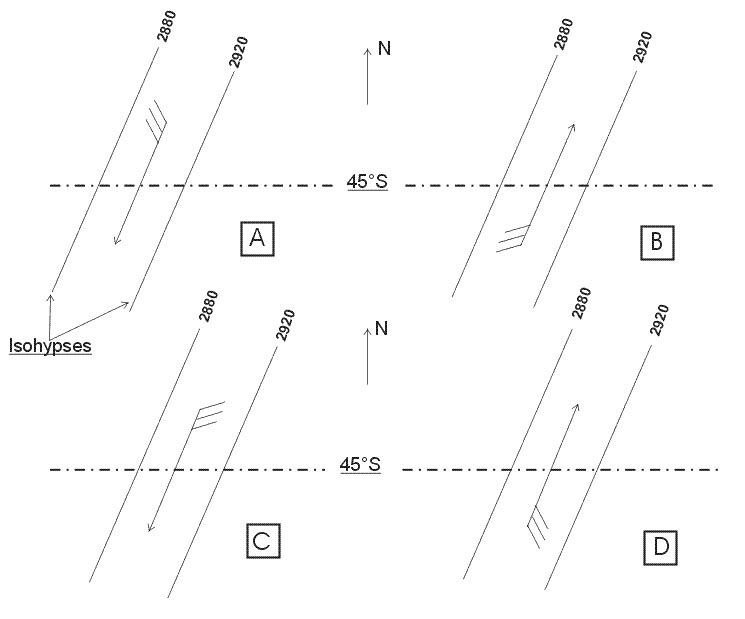special thanks to aluque for the correction exemple 374 078°.078°.

Route a b is drawn on a polar stereographic chart with the grid aligned with ?

Question 166-29 : 070° g 110° g 090° g 330° g

.at 'a' true track is 080° .convergency = change of longitude datum and 'a' meridian .convergency = 000° 010°w = 10° .convergency direction is from grid north to true north at 'a' meridian convergency direction is 10°west .convergency west = true track best .grid track = true track convergency = 080° 10°w = 070° .when passing the meridian of 050°e since the grid track is constant along the whole track the grid track remains 070° exemple 378 070°(g).070°(g).

Route a b is drawn on a polar stereographic chart with the grid aligned with ?

Question 166-30 : 090° g 110° g 070° g 150° g

. /com en/com061 621 jpg.at 'a' true track is 080° .convergency = change of longitude datum and 'a' meridian .convergency = 000° 010°w = 10° .convergency direction is from grid north to true north at 'a' meridian convergency direction is 10°east .convergency east = true track least .grid track = true track + convergency = 080° + 10°e = 090° .when passing the meridian of 050°e since the grid track is constant along the whole track the grid track remains 090° exemple 382 090°(g).090°(g).

A straight line from a 53°n 155°w to b 53°n 170°e is drawn on a lambert ?

Question 166-31 : 260° 257 5° 100° 102 5°

.change of longitude between a and b is 155°w to 170°e by the oppposite greenwich meridian = 35°.rhumb line track from a to b is 270°true .difference between great circle track and rhumb line track at a specified position is called conversion angle .the value of conversion angle can be calculated as half the value of convergency and convergency = difference of longitude x sin mean latitude ..the great circle track at a is .270° + conversion angle.conversion angle = 0 5 x 35° x sin 53° = 14°.departure track great circle is 270° + 14 ° = 284°..from a to the meridian 175°e the great circle track decreases by convergency .284° difference of longitude x sin mean latitude .difference of longitude = 155°w to 175°e = 30°.284° 30° x sin53° = 284° 24° = 260° exemple 386 260°.260°.

A route is flown from 80°s 100°w to 80°s 140°e at 160°w the grid track gt ?

Question 166-32 : 290° g and 270° t 270° g and 290° t 110° g and 270° t 270° g and 110° t

. /com en/com061 636 jpg. exemple 390 290°(g) and 270°(t).290°(g) and 270°(t).

Given .position ndb 55°10'n 012°55'e .dead rekoning position 54°53'n ?

Question 166-33 : 262° 272° 258° 265°

Admin .the rmi indicates the ndb direction we have to applie variation and convergency .bearing is measured at the aricraft since it is a ndb variation is applied at the aircraft . 090° 10° 'variation west magnetic best' .convergency = difference of longitude x sin mean latitude .between us and the ndb difference of longitude is 012°55' 009°58' = 2°57' = 2 95°.mean latitude is 40+48 /2 = 44°n .convergency = 2 95° x sin 44° = 2° .080° + 2° = 082° .the direction of the bearing to be plotted from the ndb is 082° + 180° = 262° exemple 394 262°.262°.

An aircraft is at position 53°n 006°w and has a landmark at position 52°47'n ?

Question 166-34 : 278° 277° 276° 250°

. /com en/com061 639a jpg.true track is 037° .relative bearing of the landmark 037° + 060° = 097° .standard parallels of the chart are 37°n and 65°n the parallel of origin is . 37+65 / 2 = 51°n .convergency = change of longitude x sin parallel of origin.convergency = 006° 4 75° x sin51°.convergency = 1 25° x 0777 = 1° .true track at the aircraft position is 097° the true track at the landmark is more than 97° . /com en/com061 639b jpg.thus you must add the 1° of convergency .097° + 1° + 180° bearing from the landmark = 278° exemple 398 278°.278°.

A vor is situated at position 74°n 094°w .local variation is 50°w .a polar ?

Question 166-35 : 103° 283° 013° 193°

. /com en/com061 640 jpg.without calculation answer 103° appears to be the correct one .by calculation .magnetic track 238° 180° = 058°.true track 058° variation 50°w = 008° .convert magnetic track to grid track using grivation .sum of convergency and magnetic variation.sum of convergency= 94°e.magnetic variation= 50°w.94°e 50°w = 44°e.058° + 44° e = 102° exemple 402 103°.103°.

Thule vor is located at 76°32'n 68°15'w a polar stereographic chart with the ?

Question 166-36 : 023° g 285° g 203° g 323° g

Schaverius .use formula for grid navigation .grid heading = true heading + west longitude or east longitude.the radial inbound r210 outbound is a magnetic heading of 030° 210 180 .subtract variation to find true .030 75 = 315° true.now apply the formula .grid = 315 + 68°15' = 23 25°grid exemple 406 023°(g)023°(g)

Route a b is drawn on a southern polar stereographic chart whose grid is ?

Question 166-37 : 190° g 350° g 120° g 030° g

. /com en/com061 643 png.when passing the meridian of 100°e the true track is 090° .since the grid is aligned with the greenwich meridian 100° + 090° = 190° grid exemple 410 190°(g).190°(g).

The constant of the cone in a lambert chart is 0 8666500 the angle between the ?

Question 166-38 : 4 3° 5 0° 5 8° 10 0°

Admin .change of longitude = 023° 018° = 005° .constant of the cone is 0 8666500.convergency = change of longitude x constant of the cone.convergency = 005° x 0 8666500 = 4 3° exemple 414 4.3°4.3°

Given .lambert conformal conical projection scale 1 1 234 000 standard ?

Question 166-39 : Is less than 54 19 cm is 56 66 cm is more than 57 13 cm is between 54 19 cm and 57 13 cm

Admin .at the exam only lambert conformal charts mathematically produced with two standard parallels will be considered .distance on earth = 10° x 60 x cos 53° = 361 nm.361 nm x 1 852 km = 668 73 km = 66 873 000 cm.scale = chart lenght/earth distance.scale = chart lenght/66 873 000 cm = 1/1 234 000.chart lenght = 66 873 000 / 1 234 000 = 54 19 cm.on a lambert conformal conic projection scale indicated on the chart will be correct at the standard parallels scale within the standard parallels differs by less than 1% from the scale stated on the chart .the parallel of origin is close to the mean latitude between the standard parallels and the scale will increase away from the parallel of origin if the scale increase to reach the scale stated on the chart it means that at the parallel of origin the scale is less than the scale stated on the chart .thus the distance on the map between position a and position b measured along the rhumb line is less than 54 19 cm exemple 418 Is less than 54.19 cm.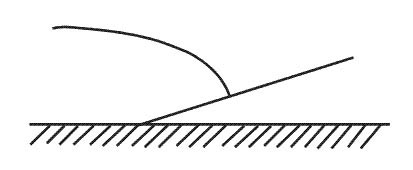Is less than 54.19 cm.

Two places are situated on the same parallel in the southern hemisphere the ?

Question 166-40 : The great circle is situated between the parallel and the straight line because the concave side of the great circle is always pointed towards the pole the correct sequence from north to south is great circle straight line rhumb line the rhumb line is situated between the great circle and the straight line because the shortest distance between to places on earth is the great circle the great circle is situated between the parallel and the straight line because the concave side of the great circle is always pointed towards the equator

Admin . 1777 exemple 422 The great circle is situated between the parallel and the straight line, because the concave side of the great circle is always pointed towards the pole.The great circle is situated between the parallel and the straight line, because the concave side of the great circle is always pointed towards the pole.

~

Exclusive rights reserved. Reproduction prohibited under penalty of prosecution.

6599 Free Training Exam