Un compte Premium offert sur le site FCL.055 ! Rendez-vous sur www.fcl055-exam.fr puis créez un compte avec le même email que celui... [Lire la suite]

A mercator chart has a scale at the equator = 1 3 704 000 what is the scale at ? [ Formation assignment ]

Question 163-1 : 1 1 852 000 1 7 408 000 1 3 208 000 1 185 200

exemple 263 1: 1 852 000 — Admin .at 60°s scale is = 1 3 704 000 x 1 / cos60°.scale = 1 3 704 000 x 1 / 0 5.scale = 1 / 3 704 000 x 0 5 .scale = 1 1 852 000 1: 1 852 000

The distance measured between two points on a navigation map is 42 mm ?

Question 163-2 : 36 30 nm 370 00 nm 67 20 nm 3 69 nm

exemple 267 36.30 nm. — .1 mm on the map = 1 600 000 mm on the ground .1 600 000 mm = 1 6 km.1 6 km / 1 852 = 0 864 nm.1 mm on the map = 0 864 nm on the ground.42 mm = 0 864 x 42 = 36 28 nm 36.30 nm.

The standard parallels of a lambert's conical orthomorphic projection are ?

Question 163-3 : 0 39 0 6 0 92 0 42

exemple 271 0.39 — Admin .constant of cone convergency factor the ratio between the top angle of the unfolded cone and 360° or sine of the parallel of origin .the parallel of origin is about half way between the standard parallels .midway between 07°40'n and 38°20'n is 23° .sin of 23° = 0 39 0.39

On a lambert conformal conic chart the convergence of the meridians ?

Question 163-4 : Is the same as earth convergency at the parallel of origin is zero throughout the chart varies as the secant of the latitude equals earth convergency at the standard parallels

exemple 275 Is the same as earth convergency at the parallel of origin. — Admin .on a lamberts chart scale is correct at the standard parallels where the cones slices through the surface of the globe and convergency is correct along the parallel of origin and the constant of the cone or convergence factor is the sine of the parallel of origin Is the same as earth convergency at the parallel of origin.

A straight line drawn on a chart measures 4 63 cm and represents 150 nm the ?

Question 163-5 : 1 6 000 000 1 5 000 000 1 1 000 000 1 3 000 000

exemple 279 1: 6 000 000. — Admin .150 nm x 1 852 = 277 8 km.277 8 km x 1000 = 277 800 m.277 800 m x 100 = 27 7800 000 cm.27 7800 000 cm / 4 63 cm = 6 000 000 1: 6 000 000.

On a polar stereographic chart the initial great circle course from a 70°n ?

Question 163-6 : 030° t 210° t 330° t 150° t

exemple 283 030°(t). — Admin . 1386.conversion angle formula is not accurate for long distances .but we can try .conversion angle 1/2 g sin lm.g change of longitude 120° .lm = mean latitude 70° .conversion angle = 1/2 x 120 x sin70 = 56°.090° rhumb line 56° = 034° 030°(t).

On a lambert conformal conic chart great circles that are not meridians are ?

Question 163-7 : Curves concave to the parallel of origin straight lines regardless of distance curves concave to the pole of projection straight lines within the standard parallels

exemple 287 Curves concave to the parallel of origin. — Admin .the parallel of origin is approximately at half way between the two standard parallels . 1387. 1388.standard parallels are 20°n and 50°n parallel of origin is 30°n.meridians which are great circles are straight lines .all other great circles are curved concave to the parallel of origin . 2506 Curves concave to the parallel of origin.

On a direct mercator projection at latitude 45° north a certain length ?

Question 163-8 : 86 nm 57 nm 70 nm 81 nm

exemple 291 86 nm. — Admin .60 x cos 45 x x = 70.42 42 x x = 70. x = 70 / 42 42 = 1 65.60 x cos 30 x 1 65 = 86 nm .ducksherminator .i'd just like to give the method i used to find the answer i personnaly find it easier . 70/cos45° x cos30° = 85 73 86 nm.

On a polar stereographic projection chart showing the south pole a straight ?

Question 163-9 : 225° 135° 250° 315°

exemple 295 225°. — Admin .draw the situtation . 1389 225°.

On a direct mercator projection the distance measured between two meridians ?

Question 163-10 : 1 3 500 000 1 4 750 000 1 7 000 000 1 6 000 000

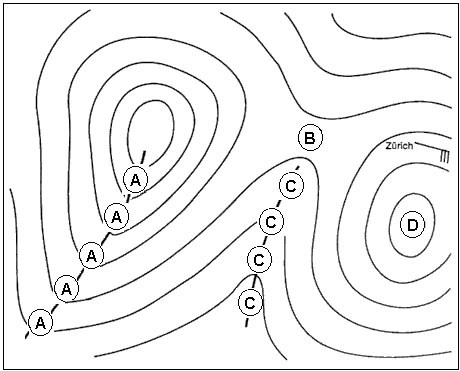exemple 299 1: 3 500 000. — Admin .scale = chart lenght/earth distance.earth distance = 5° x 60 nm x cos 60° = 150 nm.150 nm x 1 852 = 277 8 km.1 cm chart scale = 277 8 /8 = 34 725 km .1 cm 3 472 000 cm 1: 3 500 000.

Two positions plotted on a polar stereographic chart a 80°n 000° and b 70°n ?

Question 163-11 : 203° 247° 023° 305°

exemple 303 203°. — Admin .draw the situation . 1391.at the highest latitude 035°w our true course is 270° .on a polar stereographic chart convergency is equal to the change of longitude 102° 35° = 67°.270° 67° = 203° 203°.

Assume a north polar stereographic chart whose grid is aligned with the ?

Question 163-12 : 80°00'n 080°e 70°15'n 080°e 78°45'n 087°e 79°15'n 074°e

exemple 307 80°00'n 080°e. — Admin .the grid is aligned with the greenwich meridian .use meridian 090°e graduation to find distance 480 nm along the 110°e 1° = 60 nm 480/60 = 8° .next step your aircraft turn on a 154° heading grid track for a distance of 300 nm 300/60 = 5° . 1397.its position is now approximately 80°00'n 080°e 80°00'n 080°e.

The convergence factor of a lambert conformal conic chart is quoted as 0 78535 ?

Question 163-13 : 51°45' 52°05' 80°39' 38°15'

exemple 311 51°45'. — Admin .the convergency factor on a lambert chart is the sinus of the parallel of origin .n = sin l0 .0 78535 = sin parallel of origin.parallel of origin = sin 1 0 78535 = 51 75 51°45' 51°45'.

At 47° north the chart distance between meridians 10° apart is 12 7 cm the ?

Question 163-14 : 1 6 000 000 1 8 000 000 1 3 000 000 1 2 500 000

exemple 315 1: 6 000 000 — Admin .scale = chart lenght/earth distance.earth distance = 10° x 60 nm x cos 47° = 409 2 nm.409 2 x 1 852 = 758 km.1 cm chart scale = 758 / 12 7 = 60 km.1 cm 6 000 000 cm . marcinkocybik .why we substract 758 / 12 7 . .we divide because 12 7 cm on the chart corresponds to 758 km on earth and we want to now the value for 1 cm 1: 6 000 000

On a direct mercator chart a great circle will be represented by a ?

Question 163-15 : Curve concave to the equator complex curve curve convex to the equator straight line

exemple 319 Curve concave to the equator. — .on a direct mercator chart meridians a parallel equally spaced vertical straight lines . /com en/com061 514 jpg.great circle is the shortest distance between two points on earth but not on a direct mercator chart .for information . /com en/com061 394b jpg. Curve concave to the equator.

The constant of cone of a lambert conformal conic chart is quoted as 0 3955 at ?

Question 163-16 : 23°18' 66°42' 68°25' 21°35'

exemple 323 23°18'. — Admin .constant of cone convergency factor the ratio between the top angle of the unfolded cone and 360° or sine of the parallel of origin .the parallel of origin is .sin 1 or arcsin of 23° = 23 29° 23°18' 23°18'.

On a lambert conformal chart the distance between meridians 5° apart along ?

Question 163-17 : 1 5 000 000 1 3 750 000 1 2 000 000 1 6 000 000

exemple 327 1: 5 000 000 — Scale = chart lenght/earth distance.earth distance = 5° x 60 nm x cos 37° = 239 6 nm.239 6 x 1 852 = 444 km.1 cm chart scale = 444 /9 = 49 33 km.1 cm 4 933 000 cm 1: 5 000 000

The great circle bearing from a 70°s 030°w to b 70°s 060°e is approximately ?

Question 163-18 : 132° t 048° t 090° t 312° t

exemple 331 132°(t). — Admin . 1422.great circle direction at a = 090° rhumb line + conversion angle 1/2 g sin lm .conversion angle = 1/2 g sin lm.g change of longitude 90° .lm = mean latitude 70° .conversion angle = 1/2 x 90° x sin70°.conversion angle = 42°.great circle direction at a = 090° + 42° = 132° 132°(t).

In a navigation chart a distance of 49 nm is equal to 7 cm the scale of the ?

Question 163-19 : 1 1 300 000 1 700 000 1 130 000 1 7 000 000

exemple 335 1: 1 300 000 — Admin .49 nm x 1 852 = 91 km.91 / 7 = 13 km.1 cm 1 300 000 cm 1: 1 300 000

At 60°n the scale of a direct mercator chart is 1 3 000 000 what is the scale ?

Question 163-20 : 1 6 000 000 1 3 000 000 1 3 500 000 1 1 500 000

exemple 339 1: 6 000 000. — .scale at 60°n = scale at equator x 1/cos60° = 1/3 000 000 ..scale at equator = cos60°/3 000 000 .scale at equator = 1/6 000 000 1: 6 000 000.

What is the chart distance between longitudes 179°e and 175°w on a direct ?

Question 163-21 : 133 mm 106 mm 167 mm 72 mm

exemple 343 133 mm. — Admin .scale = chart distance/earth distance.earth distance = 6º = 6° x 60 nm = 360 nm at the equator.360 nm = 667 3km = 667 300 000 mm.scale = chart distance / 667 300 000 = 1/5 000 000.chart distance = 667 300 000 / 5 000 000 = 133 mm .dalton .on a mercator chart 179e and 175w are not distant by 6° but by 179+175=354° . .earth is a globe longitudes 179°e and 175°w are separated by 354° or 6° 133 mm.

The total length of the 53°n parallel of latitude on a direct mercator chart ?

Question 163-22 : 1 26 000 000 1 30 000 000 1 18 000 000 1 21 000 000

exemple 347 1: 26 000 000 — Admin .on a direct mercator chart meridians are parallel so all parallels of latitude will have the same lenght .scale = chart distance / earth distance. .scale = 133 cm / 360 x 60 x cos30°.scale = 133 cm / 18706 nm = 133 cm / 34643 5 km.scale = 133 cm / 34 643 500 m.scale = 133 cm / 34 643 500 000 cm.1 cm / 26 047 744 cm 1: 26 000 000

A lambert conformal conic projection with two standard parallels ?

Question 163-23 : The scale is only correct along the standard parallels shows all great circles as straight lines the scale is only correct at parallel of origin shows lines of longitude as parallel straight lines

exemple 351 The scale is only correct along the standard parallels. — Admin .the lambert conformal is what most of today's aeronautical charts are based on . 1776.on a lamberts chart scale is only correct at the standard parallels where the cones slices through the surface of the globe and convergency is correct along the parallel of origin and the constant of the cone or convergence factor is the sine of the parallel of origin The scale is only correct along the standard parallels.

The constant of the cone on a lambert chart where the convergence angle between ?

Question 163-24 : 0 75 0 64 0 5 0 4

exemple 355 0.75 — Chart convergency = difference of longitude x constant of cone.difference of longitude = 10°e to 30°w = 40° .30° = 40° x constant of cone.constant of cone = 30/40 = 0 75 0.75

A line drawn on a chart which joins all points where the value of magnetic ?

Question 163-25 : Agonic line aclinic line isogonal isotach

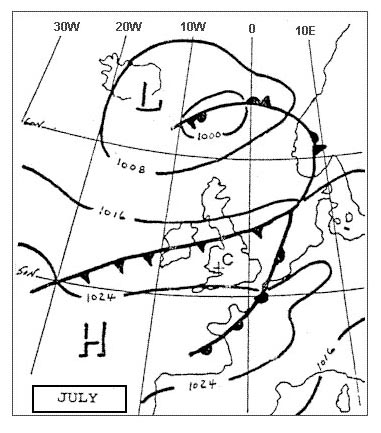exemple 359 Agonic line. — . /com en/com061 87 jpg.agonic line a line which joins all points where the value of magnetic variation is zero Agonic line.

The chart distance between meridians 10° apart at latitude 65° north is 9 5 ?

Question 163-26 : 1 5 000 000 1 6 000 000 1 2 500 000 1 3 000 000

exemple 363 1: 5 000 000 — Admin .scale = chart lenght/earth distance.earth distance = 10° x 60 nm x cos 65° = 254 nm.254 x 1 852 = 470 km.1 cm chart scale = 470 /9 5 = 49 47 km.1 cm 4 947 000 cm 1: 5 000 000

On a lambert conformal conic chart with two standard parallels the quoted scale ?

Question 163-27 : Along the two standard parallels in the area between the standard parallels along the parallel of origin along the prime meridian

exemple 367 Along the two standard parallels. — Admin .the lambert conformal is what most of today's aeronautical charts are based on . 1776.on a lamberts chart scale is correct at the standard parallels where the cones slices through the surface of the globe and convergency is correct along the parallel of origin and the constant of the cone or convergence factor is the sine of the parallel of origin Along the two standard parallels.

On a lambert conformal conic chart earth convergency is most accurately ?

Question 163-28 : Parallel of origin north and south limits of the chart standard parallels equator

exemple 371 Parallel of origin. — Admin .the lambert conformal is what most of today's aeronautical charts are based on . 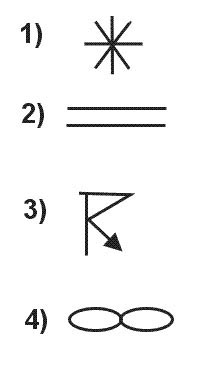1776.on a lamberts chart scale is correct at the standard parallels where the cones slices through the surface of the globe and convergency is correct along the parallel of origin and the constant of the cone or convergence factor is the sine of the parallel of origin .convergency is the angle of inclination between two selected meridians measured at a given latitude Parallel of origin.

A chart has the scale 1 1 000 000 from a to b on the chart measures 3 8 cm the ?

Question 163-29 : 20 5 205 38 70 4

exemple 375 20.5. — Admin .1 cm = 1 000 000 = 10 km.3 8 x 10 km = 38 km.38 / 1 852 = 20 5 nm 20.5.

Contour lines on aeronautical maps and charts connect points ?

Question 163-30 : Having the same elevation above sea level with the same variation having the same longitude of equal latitude

exemple 379 Having the same elevation above sea level — Having the same elevation above sea level

A rhumb line is ?

Question 163-31 : A line on the surface of the earth cutting all meridians at the same angle the shortest distance between two points on a polyconic projection any straight line on a lambert projection a line convex to the nearest pole on a mercator projection

exemple 383 A line on the surface of the earth cutting all meridians at the same angle. — . /com en/com061 101 jpg.remember .rhumb lines or loxodromes are tracks of constant true course .great circle is the shortest distance between two points A line on the surface of the earth cutting all meridians at the same angle.

A straight line on a lambert conformal projection chart for normal flight ?

Question 163-32 : Is approximately a great circle is a loxodromic line is a rhumb line can only be a parallel of latitude

exemple 387 Is approximately a great circle. — Meridians which are great circles are straight lines all other great circles are almost straight lines but curved concave to the parallel of origin rhumb lines loxodromes are curves concave to the pole Is approximately a great circle.

An aircraft flies a great circle track from 56°n 070°w to 62°n 110°e the ?

Question 163-33 : 3720 nm 5420 nm 1788 nm 2040 nm

exemple 391 3720 nm. — Admin .070°w to 180°w/e = 110°.180°w/e to 110°e = 70°.difference of longitude = 180°.it seems that this great circle track will pass by the north pole .from position 56°n 070°w we have 34° of latitude to reach the north pole from north pole to position 62°n 110°e we have 28° of latitude .34° + 28° = 62°.62° x 60 nm = 3720 nm 3720 nm.

Parallels of latitude on a direct mercator chart are ?

Question 163-34 : Parallel straight lines unequally spaced parallel straight lines equally spaced arcs of concentric circles equally spaced straight lines converging above the pole

exemple 395 Parallel straight lines unequally spaced. — Admin . 1753. direct mercator chart .parallels of latitude on a direct mercator chart are parallel straight lines unequally spaced the distance between latitudes increases away from the centre .meridians are parallel equally spaced vertical straight lines Parallel straight lines unequally spaced.

The parallels on a lambert conformal conic chart are represented by ?

Question 163-35 : Arcs of concentric circles straight lines parabolic lines hyperbolic lines

exemple 399 Arcs of concentric circles. — .the lambert conformal is what most of today's aeronautical charts are based on . /com en/com061 699 jpg. Arcs of concentric circles.

Approximately how many nautical miles correspond to 12 cm on a map with a scale ?

Question 163-36 : 130 150 329 43

exemple 403 130. — 12 cm x 2 000 000 cm = 24 000 000 cm.24 000 000 cm = 240 km.240 km / 1 852 = 130 nm 130.

A lambert conformal conic chart has a constant of the cone of 0 75 .the initial ?

Question 163-37 : 034° w 038° w 036° w 041° w

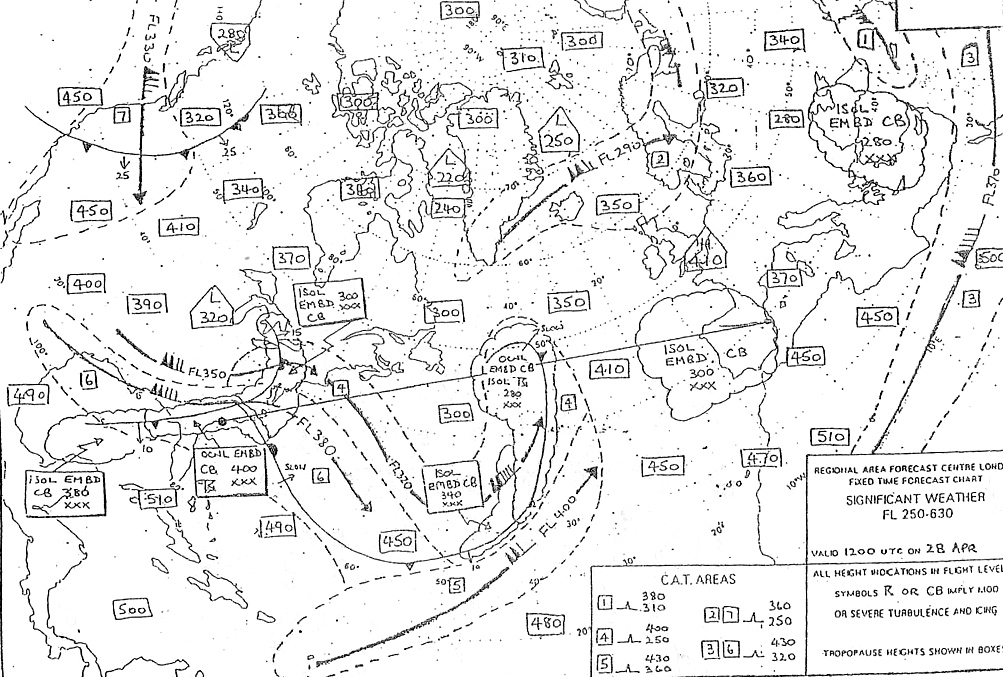exemple 407 034° w. — Admin .convergency = 055° 043° = 12°.change in longitude = convergency / n.change in longitude = 12° / 0 75 = 16°.a is at 050°w and b 34°w 50° 16° . minus 16° because we are heading east 034° w.

A lambert conformal conic chart has a constant of the cone of 0 80 .a straight ?

Question 163-38 : 011°e 009°36'e 008°e 019°e

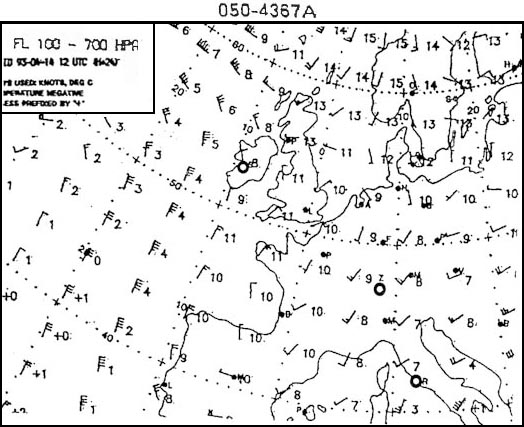exemple 411 011°e. — Admin .sin l0 = x / g.sin l0 = 0 80.x = 80° 92°= 12°.g = 12° / 0 80 = 15°.15° 4° = 11° 011°e.

What is the radial and dme distance from bel vor/dme n5439 7 w00613 8 to ?

Question 163-39 : 236° 44 nm 223° 36 nm 320° 44 nm 333° 36 nm

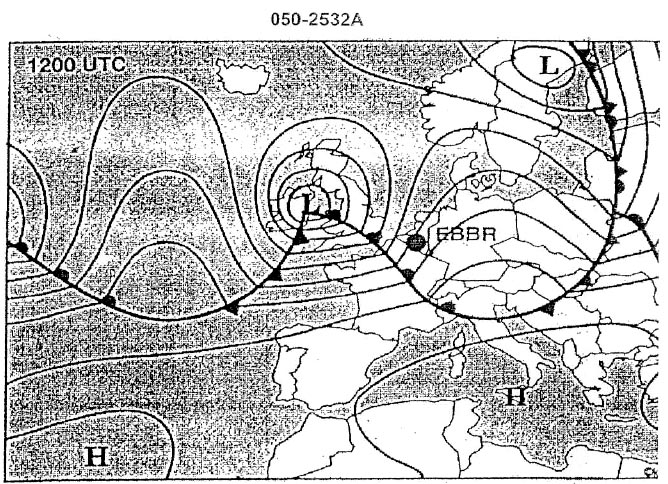exemple 415 236° - 44 nm — 236° - 44 nm

What is the radial and dme distance from bel vor/dme n5439 7 w00613 8 to ?

Question 163-40 : 278° 44 nm 090° 46 nm 278° 10 nm 098° 45 nm

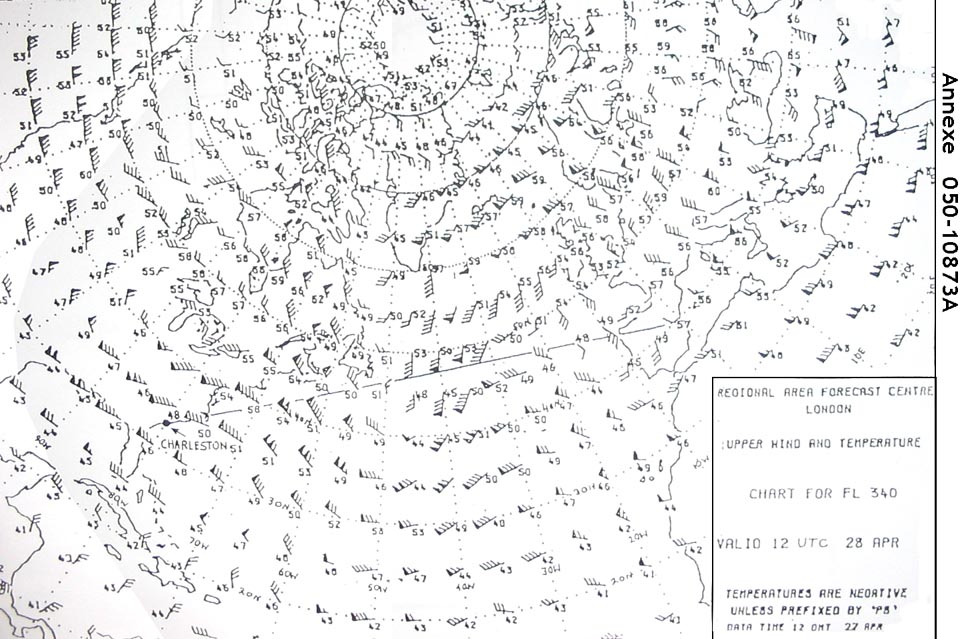exemple 419 278° - 44 nm — .plot position n5440 w00730 and draw a line from belfast vor .center your protractor you read 278° . /com en/com061 242 jpg.use the latitude scale to find 44 nm 278° - 44 nm

~

Exclusive rights reserved. Reproduction prohibited under penalty of prosecution.

6479 Free Training Exam