Un compte Premium offert sur le site FCL.055 ! Rendez-vous sur www.fcl055-exam.fr puis créez un compte avec le même email que celui...   [Lire la suite]


Which statement regarding the apparent sun and the mean sun is correct ? [ Formation assignment ]

Question 160-1 : The apparent sun is the visible sun the mean sun is a fictitious sun the apparent sun is a fictitious sun coupled to utc the mean sun is related to the local mean time the mean sun moves along the ecliptic the apparent sun along the celestial equator the apparent sun is not important for navigation as difference in time with the mean sun is maximal 4 seconds

.apparent sun 'apparent solar time' or 'true solar time' is given by the daily apparent motion of the true or observed sun it is based on the apparent solar day which is the interval between two successive returns of the sun to the local meridian .the mean sun is imaginary sun moving along the celestial equator at a constant rate and completing its annual course in the same time as the sun takes to move round the ecliptic at a varying rate it is used in the measurement of mean solar time .mean solar time conceptually is the hour angle of the fictitious mean sun the duration of daylight varies during the year the length of a mean solar day is nearly constant unlike that of an apparent solar day exemple 260 The apparent sun is the visible sun, the mean sun is a fictitious sun.The apparent sun is the visible sun, the mean sun is a fictitious sun.

The declination of the sun is defined as ?

Question 160-2 : The angular distance of the sun north or south of the celestial equator the arc of the meridian of the sun measured from the nearest pole to the sun the arc from the celestial horizon to the sun measured along a vertical line perpendicular on the horizon the arc along the celestial sphere from zenith to the sun

. /com en/com061 682 gif.directly above the equator of the earth we find the celestial equator in the sky .declination of the sun is the angular distance of the sun north or south of the celestial equator . /com en/com061 682a jpg.the earth's equator is tilted 23 5 degrees with respect to the plane of the earth's orbit around the sun so at various times during the year as the earth orbits the sun declination varies from 23 5 degrees north to 23 5 degrees south . /com en/com061 682b jpg.this gives rise to the seasons around december 21 the northern hemisphere of the earth is tilted 23 5 degrees away from the sun which is the winter solstice for the northern hemisphere and the summer solstice for the southern hemisphere around june 21 the southern hemisphere is tilted 23 5 degrees away from the sun which is the summer solstice for the northern hemisphere and winter solstice for the southern hemisphere on march 21 and september 21 are the fall and spring equinoxes when the sun is passing directly over the equator note that the tropics of cancer and capricorn mark the maximum declination of the sun in each hemisphere exemple 264 The angular distance of the sun north or south of the celestial equator.The angular distance of the sun north or south of the celestial equator.

The time interval between sunrise and sunset is dependent on ?

Question 160-3 : The declination of the sun and the latitude of the observer the date and the longitude of the observer the latitude and the longitude of the observer the inclination of the axis of the earth and the longitude of the observer

.depending on your location the times of sunrise and sunset and the length of the daylight period varies in a sine wave pattern .the axis of spin of the earth is not vertical to the plane between the earth and the sun .even though the earth spins on that axis and rotates around the sun the tilt of the axis never changes because of this the northern and southern hemispheres are exposed to more or less sunlight at different times .as a result when the top of the earth is in a position where it is closer to the sun the sun's light rays strike well above the equator resulting in summer and longer days . /com en/com061 684 gif.when it is summer in the northern hemisphere it is winter in the southern hemisphere exemple 268 The declination of the sun and the latitude of the observer.The declination of the sun and the latitude of the observer.

The definition of true north for any observer is ?

Question 160-4 : The direction of the observer's meridian to the north pole the direction of the greenwich meridian to the north pole the direction of the observer's magnetic north corrected for local variation the reading of the observer's compass corrected for deviation and local variation

.true north may in practical terms be magnetic north corrected for local variation but that is not the definition the definition is 'the direction from the observer to the geographic north pole along the local meridian' exemple 272 The direction of the observer's meridian to the north pole.The direction of the observer's meridian to the north pole.

A definition of a magnetic track angle is ?

Question 160-5 : The direction of a line referenced to magnetic north the direction of the longitudinal axis of an aircraft referenced to magnetic north the direction of the longitudinal axis of an aircraft referenced to compass north the direction of a line referenced to the isogonic line to the magnetic north pole

.magnetic track angle the angle measured in a clockwise direction between the track and magnetic north . the direction of the longitudinal axis of an aircraft referenced to magnetic north is the magnetic heading of the aircraft . the direction of the longitudinal axis of an aircraft referenced to compass north is the compass heading of the aircraft exemple 276 The direction of a line referenced to magnetic north.The direction of a line referenced to magnetic north.

The main reason for the occurrence of seasons on earth is ?

Question 160-6 : The inclination of the earth axis with regard to the plane of the ecliptic the distance between the sun and the earth the elliptical form of the orbit of the earth around the sun the length of the day as stated by the second law of kepler

Admin .the axis of the earth is currently tilted 23 5° degrees from 'vertical' this causes the northern hemisphere to be tilted toward the sun during half the year and tilted away from the sun the other half of the year this is the mechanism responsible for the seasons . 2475.the ecliptic is the apparent path of sun around the earth exemple 280 The inclination of the earth axis with regard to the plane of the ecliptic.The inclination of the earth axis with regard to the plane of the ecliptic.

The length of the apparent solar day varies continuously throughout a year this ?

Question 160-7 : The tilt of the earth's axis and the elliptical orbit of the earth around the sun the equation of time the fact that the earth is closest to the sun around the 1st of january the fact that the earth is closest to the sun around the 1st of july

exemple 284 The tilt of the earth's axis and the elliptical orbit of the earth around the sun.The tilt of the earth's axis and the elliptical orbit of the earth around the sun.

Which definition of the equator is correct ?

Question 160-8 : The equator is a greatcircle with its plane perpendicular to the earth rotational axis the equator is a greatcircle with its plane parallel to the earth rotational axis the equator is a small circle with its plane perpendicular to the earth rotational axis the equator is a small circle the plane is parallel to the earth rotational axis

exemple 288 The equator is a greatcircle with its plane perpendicular to the earth rotational axis.The equator is a greatcircle with its plane perpendicular to the earth rotational axis.

The direction 'magnetic north' at a position on the earth is ?

Question 160-9 : The direction of the horizontal component of the earth's magnetic field at that position the great circle between the position and the magnetic north pole the isogonal to the magnetic north pole the compass north at that position corrected for variation

Admin .earth's magnetic field has various distortions may not be aligned with the great circle to the magnetic pole .a freely suspended magnet will align itself with the earth's magnetic field assuming no other fields influencing the magnet the total field force t is resolved into a horizontal component force h and a vertical component force z we try to keep the magnets in a direct reading compass as close as possible to the local horizontal by suspending them below the pivot point and in some cases by adding weights to bias them for the northern hemisphere or the southern hemisphere the alignment of the horizontal component of the earth's field is therefore the azimuthal alignment of magnetic north exemple 292 The direction of the horizontal component of the earth's magnetic field at that position.The direction of the horizontal component of the earth's magnetic field at that position.

In which statement is the 'mean sun' best described ?

Question 160-10 : The mean sun is a fictitious sun coinciding each year with the apparent sun at the spring equinox and travelling along the celestial equator at uniform speed the mean sun is a fictitious sun coinciding each year with the apparent sun at the spring equinox and travelling along the ecliptic at uniform speed the mean sun is a fictitious sun the orbit of which coincides with that of the apparent sun but is corrected for mean astronomical and atmospheric refraction the mean sun is a fictitious sun the orbit of which coincides with that of the apparent sun but is corrected for the mean difference in hour angle

.easa definition . mean sun the mean sun is conceived to move eastward along the celestial equator at a rate that provides a uniform measure of time equal to the average time reckoned from the true sun .collins english dictionary . mean sun an imaginary sun moving along the celestial equator at a constant rate and completing its annual course in the same time as the sun takes to move round the ecliptic at a varying rate it is used in the measurement of mean solar time exemple 296 The mean sun is a fictitious sun coinciding each year with the apparent sun at the spring equinox and travelling along the celestial equator at uniform speed.The mean sun is a fictitious sun coinciding each year with the apparent sun at the spring equinox and travelling along the celestial equator at uniform speed.

Which statement about the orbit of the earth is correct ?

Question 160-11 : The orbit of the earth around the sun is an ellipse with the sun at one of the foci the orbit of the earth around the sun is a circle with the sun at its centre the orbit of the earth around the sun is an ellipse with the sun at a point halfway between the two foci the orbit of the earth is a circle with the sun at a point next to its centre

exemple 300 The orbit of the earth around the sun is an ellipse with the sun at one of the foci.The orbit of the earth around the sun is an ellipse with the sun at one of the foci.

The reason that the solar day lasts longer than the sidereal day is that ?

Question 160-12 : Both the direction of rotation of the earth around its axis and its orbital rotation around the sun are the same the orbital track of the earth around the sun is an ellipse the sun has an own movement through the universe opposite to the movement of the earth due to the gravitational forces of celestial bodies the orbital speed of the earth around its axis diminishes slowly

A solar day is the length of time between two successive passes of the sun across the same spot in the sky e g crossing the meridian overhead that time period is on average 24 00 00 hours or one mean solar day .a sidereal day is the length of time between two successive passes of the fixed stars across the sky that time period is 23 56 04 or one sidereal day .the difference occurs because over the course of a year the earth does one revolution or 'lap' around the sun so that there must be one less solar day 365 25 per year than there are sidereal days 366 25 spread over the year comes to a difference of about four minutes each day .vdo930 exemple 304 Both the direction of rotation of the earth around its axis and its orbital rotation around the sun are the same.Both the direction of rotation of the earth around its axis and its orbital rotation around the sun are the same.

Which definition describes best the notion 'poles' ?

Question 160-13 : The poles are the points of intersection between the earth's axis and the surface of the earth the poles are the points of intersection between the surface of the earth and the extended line joining the star polaris with the centre of the earth the poles are the points on the surface of the earth which have the same distance to all points of the ecliptic the poles are the points on the surface of the earth where gravity acts under an angle of exactly 90°

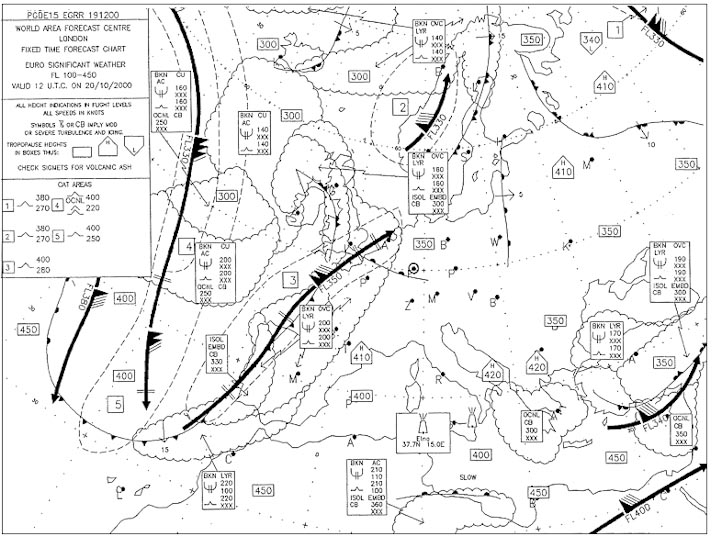.the north and south poles are at either end of the earth's axis around which the earth rotates exemple 308 The poles are the points of intersection between the earth's axis and the surface of the earth.The poles are the points of intersection between the earth's axis and the surface of the earth.

'a' latitude is 00°n/s .'b' is located at 33°n 101°e .true track great ?

Question 160-14 : 057° 123° 237° 303°

Admin . 2481.it's a great circle at 'b' latitude is 33°n departure angle at the equator = 90° 'b' latitude = 057° exemple 312 057°.057°.

Given two positions .a 56°s 010°w and b 56°s 030°w .which statement is true ?

Question 160-15 : The departure between a and b is more than great circle distance between a and b the departure between a and b is equal to or more than great circle distance between a and b the departure between a and b is less than the great circle distance between a and b the departure between a and b is equal to the great circle distance between a and b

Admin .great circle is the shortest distance between two points . 1462.easa notice distance along a parallel of latitude is also known as departure exemple 316 The departure between a and b is more than great circle distance between a and b.The departure between a and b is more than great circle distance between a and b.

Standard time for same areas is listed in the air almanac as utc +13 instead of ?

Question 160-16 : Keeping the same date as the political and or economical entity to which they belong the fact that they are keeping daylight saving time the sense of the earth rotation the setup of the sunrise/sunset tables

exemple 320 Keeping the same date as the political and or economical entity to which they belong.Keeping the same date as the political and or economical entity to which they belong.

Polar circles are line of latitude at ?

Question 160-17 : 67° n/s 60° n/s 70° n/s 80° n/s

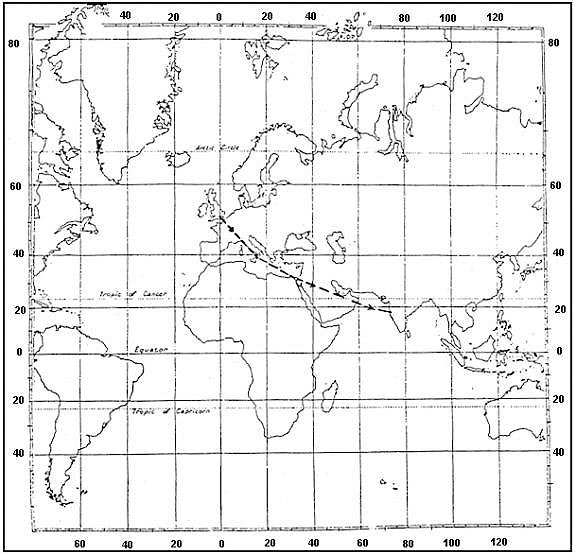Admin .polar circles are two parallels of latitude each at a distance from a pole of the earth equal to about 23 degrees 27 minutes it forms the boundary between the north temperate and north frigid zones exemple 324 67° n/s.67° n/s.

Mu'a tonga islands is situated at 21°11's 175°07'w .in the air almanac the ?

Question 160-18 : 06 59 on august 22nd 06 59 on august 21st 07 39 on august 21st 07 39 on august 22nd

Admin .sunrise at 20°s = 06 18 lmt on 21 august.sunrise at 30°s = 06 28 lmt on 21 august.sunrise at 21°s will be 06 19 lmt .conversion to utc .175°07' ==> 11h40 min 175 / 15°/h .06h39 + 11h40 = 17h59 utc .conversion to standard time .17h59 + 13 = 30h59 st .30h59 24h = 06 59 on august 22nd exemple 328 06:59 on august 22nd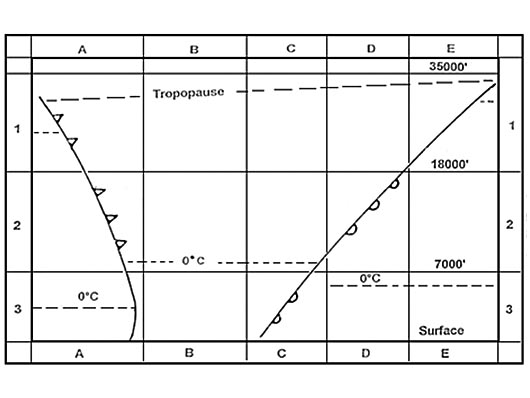.06:59 on august 22nd.

Position 'elephant point' is situated at 58°00'n 135°30'w .standard time for ?

Question 160-19 : 15 55 on january 20th 08 57 on january 21st 16 57 on january 20th 09 59 on january 21st

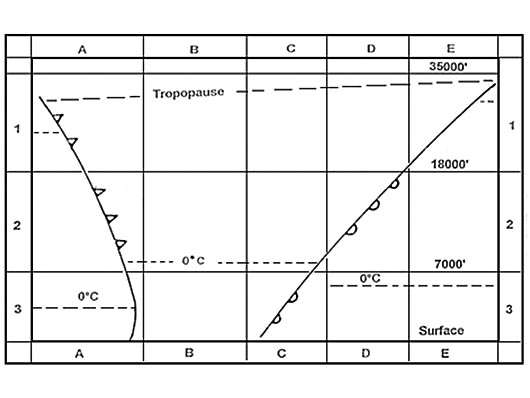.the conversion factor between lmt and utc is arc change of longitude converted to time .135°30' ==> 9h02 min 135 5 / 15°/h .00h57 9h02 = 15h55 lmt the day before january 20th exemple 332 15:55 on january 20th.15:55 on january 20th.

The direction of the earth's rotation on its axis is such that ?

Question 160-20 : Observed from the point above the north pole the rotation is counterclockwise any point on the surface of the earth will move eastward an observer on the surface of the earth always will face west when observing sunrise any point on the surface of the earth will move westward

.the earth is described as rotating from west to east if you were looking down on the north pole from space the earth would be seen to be rotating anti clockwise this is why the sun appears to rise in the east and set in the west to an observer standing on the ground the earth then rotates around the sun in an anti clockwise direction on an elliptical path exemple 336 Observed from the point above the north pole, the rotation is counterclockwise.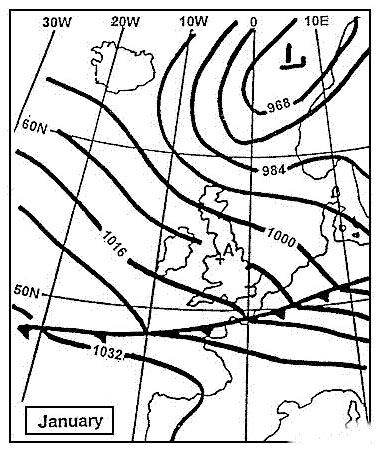Observed from the point above the north pole, the rotation is counterclockwise.

The sun's declination is ?

Question 160-21 : The sun's position relative to the plane of equator the angular distance between the sun and the celestial north pole the sun's position relative to the ecliptic the distance between the sun and the horizon

exemple 340 The sun's position relative to the plane of equator.The sun's position relative to the plane of equator.

The sun's declination is on a particular day 12°s midnight sun may this day be ?

Question 160-22 : South of 78°s north of 78°s north of 78°n at 78°s only

exemple 344 South of 78°s.South of 78°s.

The term 'sidereal' is used ?

Question 160-23 : To describe a situation or relationship concerning the stars to describe how two positions of heavenly bodies are located sideways on the sky to describe the time interval between two successive transits of the real apparent sun at the same meridian to describe conditions with reference to the moon

exemple 348 To describe a situation or relationship concerning the stars.To describe a situation or relationship concerning the stars.

The mean sun ?

Question 160-24 : Moves with constant speed along the celestial equator has a declination equal to the apparent sun is the middle position of the sun is only of interest to users of astronomical navigation

exemple 352 Moves with constant speed along the celestial equator.Moves with constant speed along the celestial equator.

In its path around the sun the axis of the earth has an inclination ?

Question 160-25 : Of 66°33' with the plane of the path varying between zero and 23°27' with the plane of the path of 23°27' with the plan of equator varying with the season of the year

Juliarmengol98 2018 02 15 as far as i understand 0 to 23º27' 23 5º would be correct if the question asked for the latitudes the sun would be directly overhead at one point during its path .as it asks for the earth's axis inclination 23 5º in relation to the plane of the earth like the equator 90º the relative angle inclination between them would be of 66º 33'~ exemple 356 Of 66°33' with the plane of the path.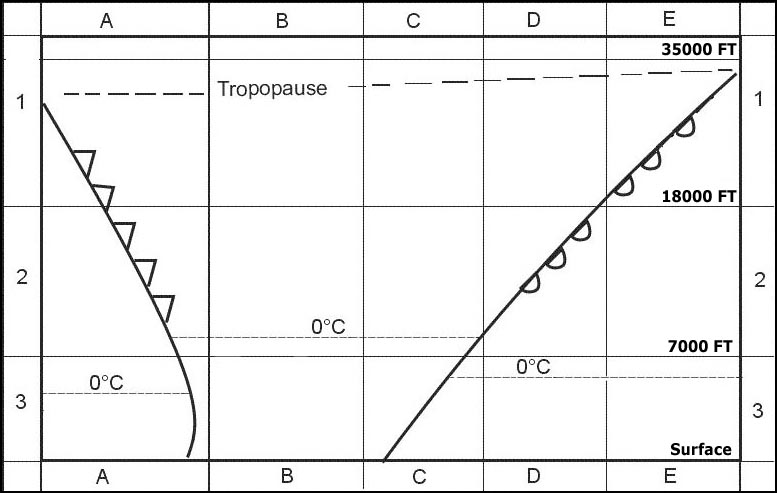Of 66°33' with the plane of the path.

As seen from an observer on the surface of the earth ?

Question 160-26 : The apparent sun is always in the plane of the ecliptic the stars will seem to move from west to east during a year the sun's position relative to the stars is fixed throughout the year the sun is in fixed position relative to the stars

.apparent sun 'apparent solar time' or 'true solar time' is given by the daily apparent motion of the true or observed sun it is based on the apparent solar day which is the interval between two successive returns of the sun to the local meridian .the plane of the ecliptic is inclined to the plane of the equator at an angle of approximately 23 5° . /com en/com061 712 jpg.from an observer on the surface of the earth the apparent sun is always in the plane of the ecliptic exemple 360 The apparent sun is always in the plane of the ecliptic.The apparent sun is always in the plane of the ecliptic.

The time it takes for the earth to complete one orbit around the sun is ?

Question 160-27 : 365 days 5 hours 48 minutes and 45 seconds 360 days 5 hours 45 minutes and 48 seconds 360 days 45 hours 5 minutes and 48 seconds 365 days 45 hours 48 minutes and 5 seconds

exemple 364 365 days, 5 hours, 48 minutes and 45 seconds.365 days, 5 hours, 48 minutes and 45 seconds.

When the sun's declination is northerly ?

Question 160-28 : The daylight period is shorter in the southern hemisphere than the northern midnight sun may be observed at the south pole the sunrise occurs earlier at southern latitudes than the northern latitudes it is winter on the northern hemisphere

exemple 368 The daylight period is shorter in the southern hemisphere than the northern.The daylight period is shorter in the southern hemisphere than the northern.

What is 'vertex' ?

Question 160-29 : The point on the great circle with greatest latitude the point on the small circle with greatest latitude the point on the great circle where it intersects the rhumb line the point on the great circle where it intersects the equator

Admin . 1718.a great circle which has an inclination of 33° to the equator reach a latitude of 33° n/s .the point on the great circle with greatest latitude is called vertex .every great circle has two vertices one in the northern hemisphere and the other in the southern hemisphere .at the 'vertex' the great circle track is 090° or 270° and it is the closest point to the pole and the farther from the equator . notice this question also exists with the following statement .'which statement about the vertex of a great circle is true .in the vertex the great circle reaches its highest latitude' exemple 372 The point on the great circle with greatest latitude.The point on the great circle with greatest latitude.

Which statement about the vertex of a great circle is always true ?

Question 160-30 : In the vertex the true track is 090° or 270° in the vertex the true heading is 090° or 270° in the vertex the true track is 090° in the vertex the true track is 270°

Admin . 1718.a great circle which has an inclination of 33° to the equator reach a latitude of 33° n/s .the point on the great circle with greatest latitude is called vertex .every great circle has two vertices one in the northern hemisphere and the other in the southern hemisphere .at the 'vertex' the great circle track is 090° or 270° and it is the closest point to the pole and the farther from the equator exemple 376 In the vertex the true track is 090° or 270°.In the vertex the true track is 090° or 270°.

A small circle ?

Question 160-31 : Has a plane that does not pass through the centre of the earth has a plane that passes through the centre of the earth is a spiral to the north pole is a random northerly track to the pole

Admin .the centre of small circles does not coincide with the centre of the earth exemple 380 Has a plane that does not pass through the centre of the earth.Has a plane that does not pass through the centre of the earth.

Spring and autumn equinox are the moments at which the sun reaches ?

Question 160-32 : A declination of 0° a declination of 23 5° a declination of 66 5° the highest declination

Ecqb03 august 2016 ..declination of the sun is the angular distance of the sun north or south of the celestial equator . /com en/com061 682a jpg.the earth's equator is tilted 23 5 degrees with respect to the plane of the earth's orbit around the sun so at various times during the year as the earth orbits the sun declination varies from 23 5 degrees north to 23 5 degrees south . /com en/com061 682b jpg.this gives rise to the seasons around december 21 the northern hemisphere of the earth is tilted 23 5 degrees away from the sun which is the winter solstice for the northern hemisphere and the summer solstice for the southern hemisphere around june 21 the southern hemisphere is tilted 23 5 degrees away from the sun which is the summer solstice for the northern hemisphere and winter solstice for the southern hemisphere on march 21 and september 21 are the spring and autumn equinoxes when the sun is passing directly over the equator a declination of 0° note that the tropics of cancer and capricorn mark the maximum declination of the sun in each hemisphere exemple 384 A declination of 0°.A declination of 0°.

An aircraft at latitude 02°20'n tracks 360° t for 685 km on completion of the ?

Question 160-33 : 08°29'n 03°50's 02°45's 06°01'n

Admin .on a meridian 1° = 60 nm .we are heading north .685 km / 1 852 = 370 nm.370 / 60 = 6 16°.0 16° x 60 = 9 6 min.02°20'n + 6°09' = 08°29'n exemple 388 08°29'n.08°29'n.

Given .a 50°n 070°w and b 50°n 080°w and the position of one of the ?

Question 160-34 : 50°06 4s 105°00 0'e 50°06 4'n 075°00 0'e 50°06 4s 075°00 0'w 50°06 4'n 105°00 0'w

exemple 392 (50°06.4s, 105°00.0'e).(50°06.4s, 105°00.0'e).

Sunrise in dublin 53°29'n 006°15'w is 06 23 lmt calculate the sunrise at ?

Question 160-35 : 06 23 07 23 05 23 07 49

Admin .difference in longitude 006°15'+008°45' = 15° .the earth moves around the sun at a rate of 4 minutes per degree of longitude 15°/h latitude remains the same only the longitude changes the sun rises at bremen airport 1h before dublin but the sun rises at the same local mean time exemple 396 06:23.06:23.

Calculate the difference in lmt between dublin 53°29'n 006°15'w and bremen ?

Question 160-36 : 01h 00m 02h 00m 00h 00m 03h 00m

Admin .difference in longitude 006°15'+008°45' = 15° .the earth moves around the sun at a rate of 4 minutes per degree of longitude 15°/h .4x15 = 60 minutes exemple 400 01h 00m.01h 00m.

Calculate the approximate distance from waypoint dbu 53°29 0'n 000°28 6'w to ?

Question 160-37 : 329 4 nm 284 nm 385 5 nm 304 2 nm

Admin .latitude difference 53°29 0'n 53°09 0'n = 20'. 20'x1°/60'=0 33° .if 0 33°x60nm/1°=20nm it could be our waypoint .longitude difference 008°45 0'e + 000°28 6'w = 9 22°.distance = change longitude x 60nm x lat wpt = 9 22° x 60nm x cos53 48° = 329 2 nm .andresmarina .it is said 20 nm of north of bremen airport .as you know 1 degree = 60 mins and 1 degree = 60 nm so 1 min = 1 nm .because of that the waypoint is located at the same latitude than dbu waypoint in this case we should use the rhumb line formula .d = change in long * 60* cos lm .d = 9 2266 * 60 * cos 53 5 = 329 2939 nm exemple 404 329.4 nm.329.4 nm.

Calculate the approximate distance from dublin 53°29 0'n 006°15 3'w to a ?

Question 160-38 : 535 7 nm 435 9 nm 565 2 nm 636 6 nm

Admin .dublin > bremen = 15°.1°=60nm on the equator.1°=60nm x cos mean latitude .1°=60nm x cos 53 33° .1°=35 844nm.15° x 35 844 = 537 66 nm.the closest answer 535 7 nm exemple 408 535.7 nm.535.7 nm.

Route a 53°24'n 015°54'e to b 32°00'n 052°51'w .distance flight plan is ?

Question 160-39 : 08 00 st a 05/08 14 00 st a 04/08 03 00 st a 05/08 05 00 st a 05/08

Admin .flight time . 3150x60 /450=7h.eta b .10 00 st 5 aug .change to utc utc+4 =10+4=14 00 utc 5 aug .departure time .14 00 7h flight time =07 00 st 5 aug .etd a .07 00 st 5 aug .change to utc utc+1 =08 00 utc 5 aug exemple 412 08:00 st(a) 05/08.08:00 st(a) 05/08.

In producing chart projections the following projection surfaces may be used ?

Question 160-40 : Plane cylinder cone plane sphere cone cylinder sphere plane parabola cone plane cylinder

exemple 416 Plane, cylinder, cone.Plane, cylinder, cone.

~

Exclusive rights reserved. Reproduction prohibited under penalty of prosecution.

6359 Free Training Exam