Un compte Premium offert sur le site FCL.055 ! Rendez-vous sur www.fcl055-exam.fr puis créez un compte avec le même email que celui...   [Lire la suite]


A 10 00 utc 2 avions sont au 87°n 000°e/w un avion part vers l'ouest à 120 ? [ Revision vol ]

Question 139-1 : 14 02 utc 13 02 utc 17 42 utc 15 02 utc

Papayou76 .voici mon raisonnement . peut être un peu mathématique mais je n'ai pas trouvé plus simple .petit cercle loxodromique parcouru par les deux avions .60x360°xcos87°=1130nm = c.soit a avion à va=160kt b avion à vb=120kt.soit da la distance parcourue par a sur le petit cercle.soit db la distance parcourue par b sur le petit cercle.da+db=c.soit t le temps pour se rejoindre.on a t=da/va=db/vb.da=dbxva/vb.da= c da va/vb. .da=cxva/ va+vb =645nm > 645/va=645/160=4 037 heures.hea 14h02 exemple 239 14:02 utc.14:02 utc.

La durée du crépuscule civil est ?

Question 139-2 : Calculée entre le coucher du soleil et le moment où le centre du soleil se situe 6° sous l'horizon vrai calculée entre le coucher du soleil et le moment où le centre du soleil se situe 12° sous l'horizon vrai calculée entre les positions apparentes du soleil de 0° et 6° fixée à 12 minutes par les autorités aéronautiques internationales

Un aéronef survole ho 55°30'n 060°15w d'où il reçoit le vor yyr 53°30'n ?

Question 139-3 : 028° 208° 031° 332°

Admin .les deux points sont sur le même méridien 060°15'w et espacés de 2° de latitude ho est au nord du vor yyr ho est dans le 000° vrai de yyr .lorsqu'on parle de vor on doit appliquer la déclinaison magnétique au vor . variation west magnetic best donc 000° + 28°w = 028° exemple 247 028°.028°.

Un aéronef dans l'hémisphère nord effectue un virage au taux 1 par la droite ?

Question 139-4 : Plus que 225° 225° moins que 225° plus ou moins de 225° selon le mode de suspension utilisé

Admin .au taux 1 vous parcourez 3°/seconde soit pour 30 secondes un virage de 90° l'aéronef sera donc à un cap de 135° + 90° = 225° .dans l'hémisphère nord lorsqu'on tourne en direction du sud le compas indiquera plus c'est ever see the south qui s'applique ici exemple 251 Plus que 225°.Plus que 225°.

Un repère apparaît à 30° à gauche de la ligne de foi de l'écran radar ?

Question 139-5 : 160° 220° 130° 310°

Admin .cap magnétique 355°.déclinaison magnétique 15° e.cap vrai 010°.relèvement à 30° à gauche.relèvement vraie de l'île depuis l'avion est donc = 340°.pour obtenir le relèvement depuis l'île on inverse le cap de 180º soit 160° .david33 .comment trouver vous le cap vrai à 010° il n'y a aucun moyen de savoir comment vous le deduisez .merci . .cap magnétique 355 + 15° de déviation est = 010° exemple 255 160°.160°.

Lors d'un virage à droite du cap 330° vers le cap 040° dans l'hémisphère ?

Question 139-6 : Sous estimera le virage et le remous augmentera l'effet sur estimera le virage et le remous diminuera l'effet sous estimera le virage et le remous diminuera l'effet sur estimera le virage et le remous augmentera l'effet

Admin .la boussole sphérique dans le cadre 'flotte' dans un liquide . 1750.aeroman52 .retenez pour la boussole .nord paresseuse sud nerveuse exemple 259 Sous-estimera le virage et le remous augmentera l'effet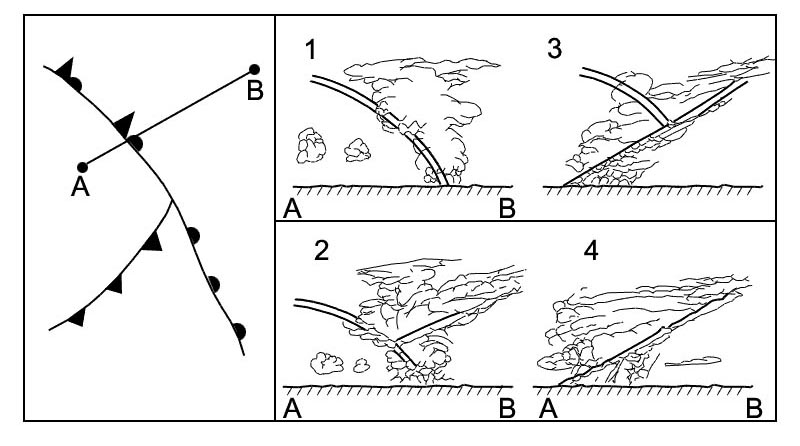.Sous-estimera le virage et le remous augmentera l'effet.

Un compas à lecture directe doit être balancé quand ?

Question 139-7 : Il y a un changement important et permanent de latitude magnétique il y a un changement important de longitude magnétique l'aéronef est stocké pour une longue durée et fréquemment déplacé l'aéronef a effectué plus d'un certain nombre d'atterrissages

Ajyh91 .par 'balancé' vous entendez 'mis à la poubelle' . .le terme 'balancé' correspond à l'action d'équilibrage/réglage du compas d'ailleurs on ne balance plus rien aujourd'hui on recycle .l'attraction magnétique terrestre variant en fonction de la latitude il est nécessaire de ré équilibrer le compas quand celle ci varie de façon importante et permanente .note cette question existe aussi à l'examen avec la réponse . 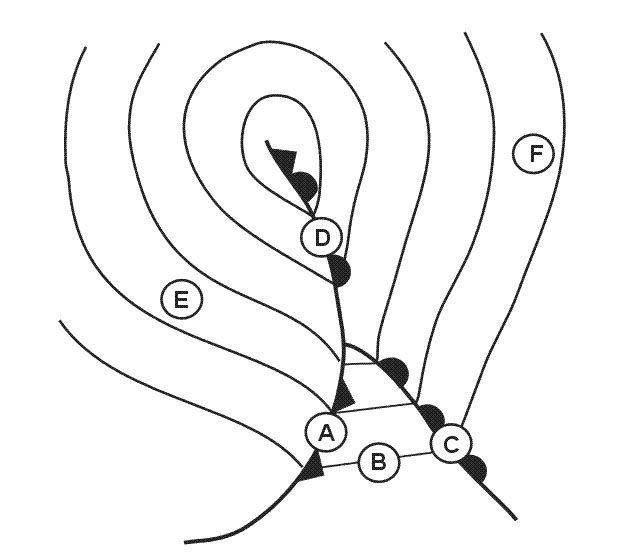une période de 12 mois s'est écoulée pendant laquelle l'aéronef est resté immobile au sol exemple 263 Il y a un changement important et permanent de latitude magnétique.Il y a un changement important et permanent de latitude magnétique.

On donne .route vraie 348°.dérive 17° gauche.déclinaison magnétique ?

Question 139-8 : 033° 007° 359° 337°

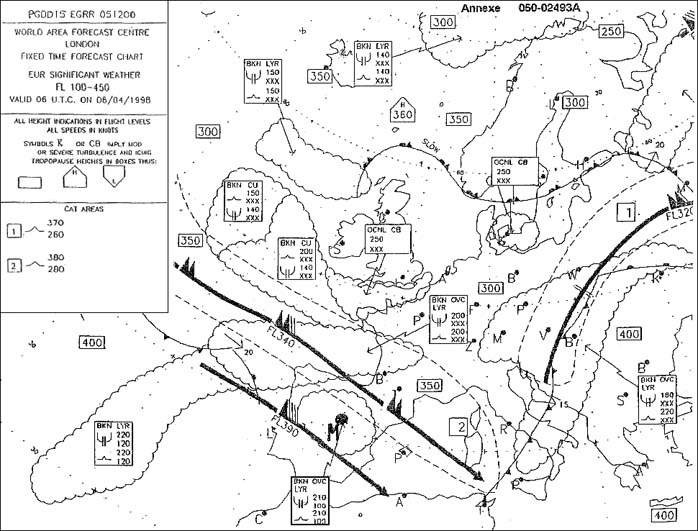Admin . 1727.insérez les valeurs de la question dans le tableau vmc rc on ajoute dans le sens indiqué par la flèche on soustrait dans l'autre sens exemple 267 033°.033°.

L'affirmation correcte concernant l'effet des erreurs en virage sur un compas ?

Question 139-9 : Les erreurs en virage sont plus importantes aux caps nord et sud et aux grandes latitudes les erreurs en virage sont plus importantes aux caps est et ouest et moindres aux grandes latitudes les erreurs en virage sont plus importantes aux caps nord et sud et moindres aux grandes latitudes les erreurs en virage sont plus importantes aux caps est et ouest et aux grandes latitudes

exemple 271 Les erreurs en virage sont plus importantes aux caps nord et sud et aux grandes latitudes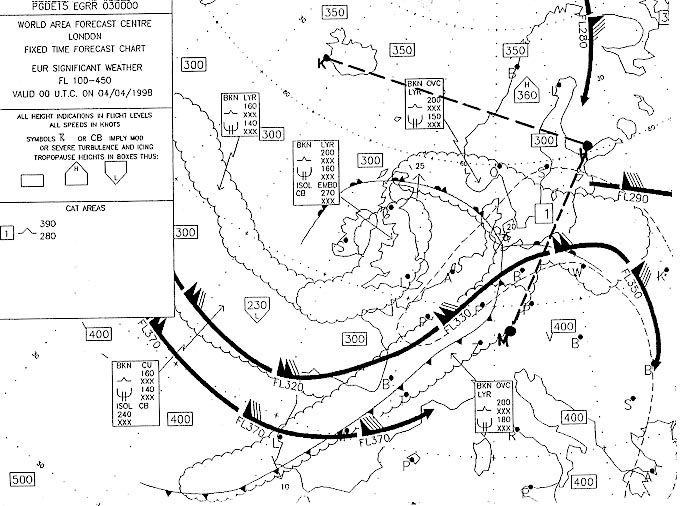.Les erreurs en virage sont plus importantes aux caps nord et sud et aux grandes latitudes.

Un compas magnétique est le plus précis ?

Question 139-10 : à mi distance des pôles magnétiques dans la région du pôle magnétique sud dans la région du pôle magnétique nord à l'équateur géographique

Admin . 1430.la force agissant sur l'aiguille d'un compas magnétique est directement proportionnelle à la composante horizontale du champ magnétique terrestre et inversement proportionnelle à la composante verticale aussi le compas magnétique sera plus précis à mi distance des pôles magnétiques c'est à dire sur l'équateur magnétique soit 'à mi distance des pôles magnétiques' et non pas géographique exemple 275 à mi-distance des pôles magnétiques.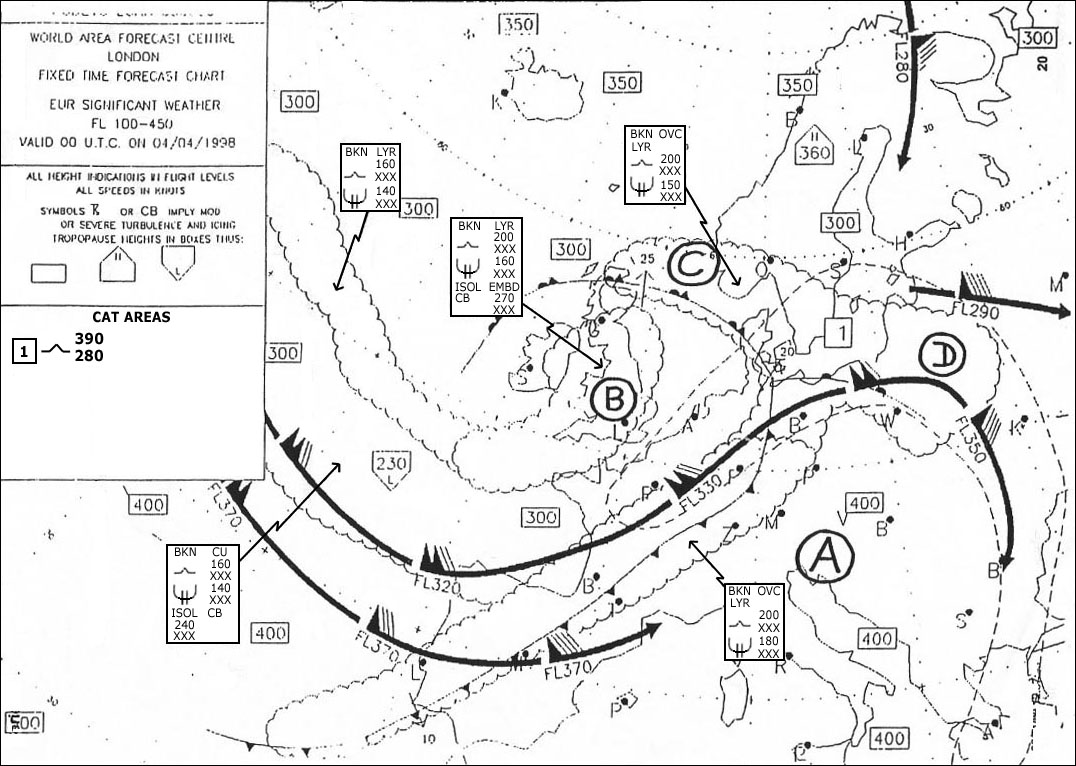à mi-distance des pôles magnétiques.

On donne .route vraie 180°.dérive 8° droite.cap compas 195°.déviation ?

Question 139-11 : 21°w 25°w 5°w 9°w

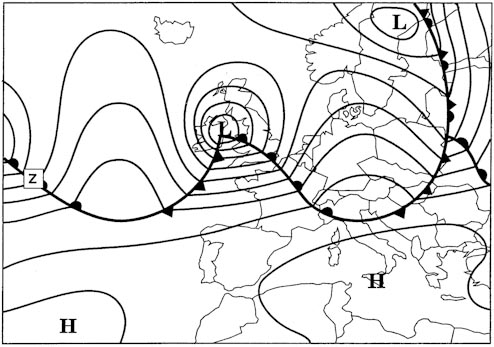Admin . 1426.insérez les valeurs de la question dans le tableau vmc rc on ajoute dans le sens indiqué par la flèche on soustrait dans l'autre sens exemple 279 21°w.21°w.

Le but de la régulation d'un compas est de ?

Question 139-12 : Mesurer l'angle entre le nord magnétique et le nord compas annuler les effets des champs magnétiques mesurés à bord de l'aéronef annuler la composante verticale du champ magnétique terrestre annuler la composante horizontale du champ magnétique terrestre

Sees9610 .la formulation n'est elle pas litigieuse .la mesure de l'angle entre le nord magnétique et le nord compas ne serait il pas le 'moyen' d'effectuer cette régulation et d'établir une courbe de déviation . 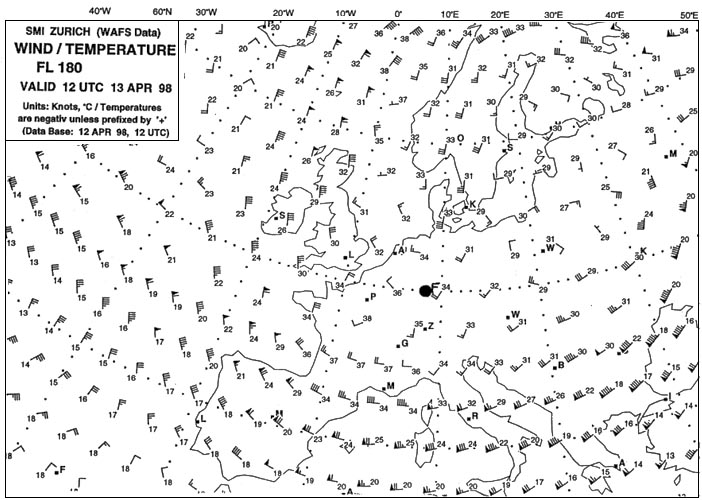.non pour nous rien de litigieux ici le but de la régulation 'calibration' en anglais est bien de mesurer la déviation du compas en établissant une courbe de déviation et d'établir avec les résultats un tableau de correction de déviation exemple 283 Mesurer l'angle entre le nord magnétique et le nord compas.Mesurer l'angle entre le nord magnétique et le nord compas.

On donne .route vraie 300°.dérive 8° droite.déclinaison magnétique 10° ?

Question 139-13 : 306° 322° 294° 278°

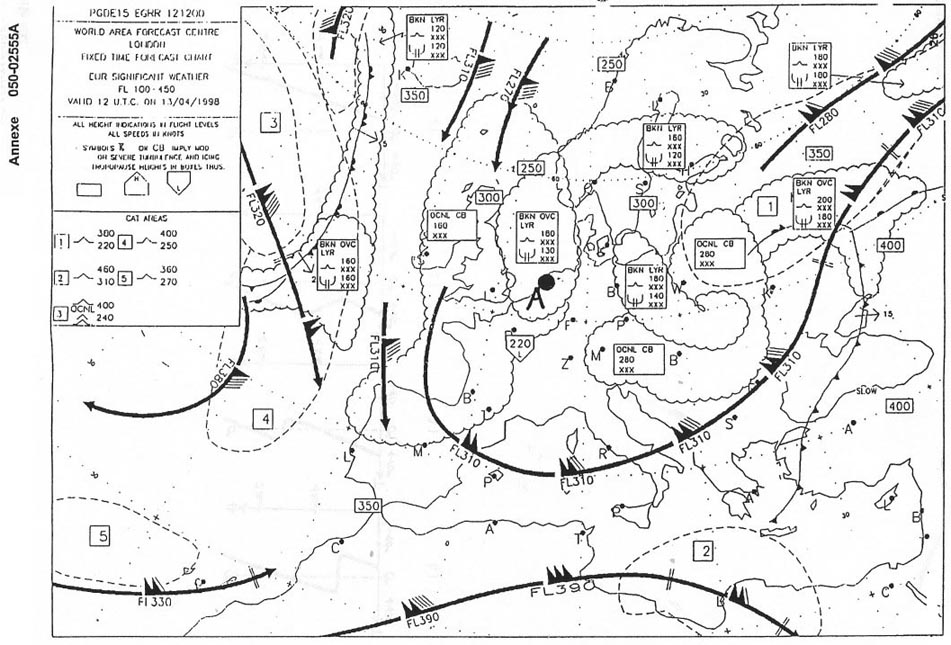exemple 287 306°.306°.

On donne .route vraie 070°.déclinaison magnétique 30°w.déviation ?

Question 139-14 : 089° 091° 100° 101°

Admin . 1769.nous vous recommandons l'utilisation de ce tableau pour éviter les erreurs exemple 291 089°.089°.

Une île est observée à 15° sur la gauche .le cap magnétique de l'aéronef ?

Question 139-15 : 268° 088° 122° 302°

Admin .voici le raisonnement à suivre .cap magnétique de l'avion 120º.déclinaison 17° w.cap vrai 103º.relèvement 15º gauche.relèvement vraie route vraie de l'île vers l'avion = 088° + 180° = 268° .evasion .il me semble que c'est le gisement=15° gauche et non le relèvement . .le gisement se compte toujours dans le sens des aiguilles d'une montre ici le gisement de l'île est de 345° .nous employons le mot 'relèvement' par simplification dans l'explication d'après l'intitulé de la question qui indique une île est observée à 15° sur la gauche exemple 295 268°.268°.

Un repère au sol est observé avec un gisement de 315° et 3 min plus tard ?

Question 139-16 : 9 nm 12 nm 3 nm 6 nm

Admin . 1392.315 270 = 45° parcouru en 3 minutes.180kt / 60 minutes = 3 nm par minute.3 min x 3 nm = 9 nm .c'est un triangle isocèle deux côtés ont la même distance 3 minutes à 180 kt soit 3 nautiques/minute soit 9 nm pour 3 minutes de vol .soval974 .tan 45° x 9 = 9 nm exemple 299 9 nm.9 nm.

Une île est observée à 15° sur la gauche .le cap magnétique de l'aéronef ?

Question 139-17 : 088° 122° 268° 302°

Admin .voici le raisonnement à suivre .cap magnétique de l'avion 120°.déclinaison 17°w.cap vraie 103°.relèvement 15° gauche.relèvement vraie de l'avion vers l'île ou route vraie de l'avion vers l'île 088° .lionel .15° gauche correspond au gisement . .non le gisement correspond à 360 15° = 345° .le gisement se compte toujours par la droite exemple 303 088°.088°.

Aligné sur une piste 05 d'orientation 047° un compas à lecture directe doit ?

Question 139-18 : 042° à 052° 045° à 049° 037° à 057° 032° à 062°

exemple 307 042° à 052°.042° à 052°.

Une déclinaison magnétique ouest négative signifie que ?

Question 139-19 : Le nord vrai est à l'est du nord magnétique le nord vrai est à l'ouest du nord magnétique le nord compas est à l'est du nord magnétique le nord compas est à l'ouest du nord magnétique

Admin .une déclinaison magnétique ouest signifie que le nord magnétique est à l'ouest du nord vrai ou que le nord vrai est à l'est du nord magnétique . 1417.les anglais ont cette formule magique variation west magnetic best déclinaison ouest magnétique plus fort qui dit que votre cap mesuré dans le sens des aiguilles d'une montre à partir du nord magnétique est plus fort que votre cap mesuré à partir du nord vrai .par convention une déclinaison magnétique ouest est négative c'est ce que vous devez déduire à votre cap magnétique pour obtenir votre cap vrai exemple 311 Le nord vrai est à l'est du nord magnétiqueLe nord vrai est à l'est du nord magnétique

Le but de la régulation compas est de pouvoir déterminer la déviation ?

Question 139-20 : à n'importe quel cap pour un cap donné seulement à n'importe quelle latitude au nord au sud à l'est et à l'ouest uniquement

exemple 315 à n'importe quel cap.à n'importe quel cap.

On donne .cap compas 265°.déclinaison magnétique 33°w.déviation 3°e.le ?

Question 139-21 : 235° 229° 301° 295°

exemple 319 235°.235°.

Un ndb est situé à la position n55°26' w005°42' .la déclinaison ?

Question 139-22 : 112 5° 108 5° 110 5° 114 5°

Admin .pour un vor la déclinaison est appliquée à la station .pour un ndb la déclinaison est appliquée à l'aéronef pour cette question on ajoute la déclinaison à l'avion soit 101 5 + 11° = 112 5 exemple 323 112,5°.112,5°.

La déviation du compas secours est ?

Question 139-23 : Dépendante du cap de l'aéronef est indépendante de la latitude de la position de l'aéronef zéro sur l'équateur magnétique positive si le nord compas est à l'ouest du nord magnétique

exemple 327 Dépendante du cap de l'aéronef.Dépendante du cap de l'aéronef.

La table de déviation d'un compas est la suivante .cm 000 030 060 090 120 150 ?

Question 139-24 : 164° 165° 146° 145°

Admin .cap compas 155° à suivre => cap magnétique à suivre => cap lu à suivre .cc 155° => cm 155° + 10° = 165°.la correction sur la table de déviation est ente 150° et 180° de 0 à 2° donc à mi chemin on retranche 1° ce qui nous fait 164° de cap compas à suivre exemple 331 164°.164°.

La table de déviation d'un compas est la suivante .cm 000 030 060 090 120 150 ?

Question 139-25 : 262° 214° 218° 258°

exemple 335 262°.262°.

Durant les vérifications avant le décollage l'indication du compas secours ?

Question 139-26 : 1 et 2 1 4 et 5 1 2 3 4 et 5 1 2 et 3

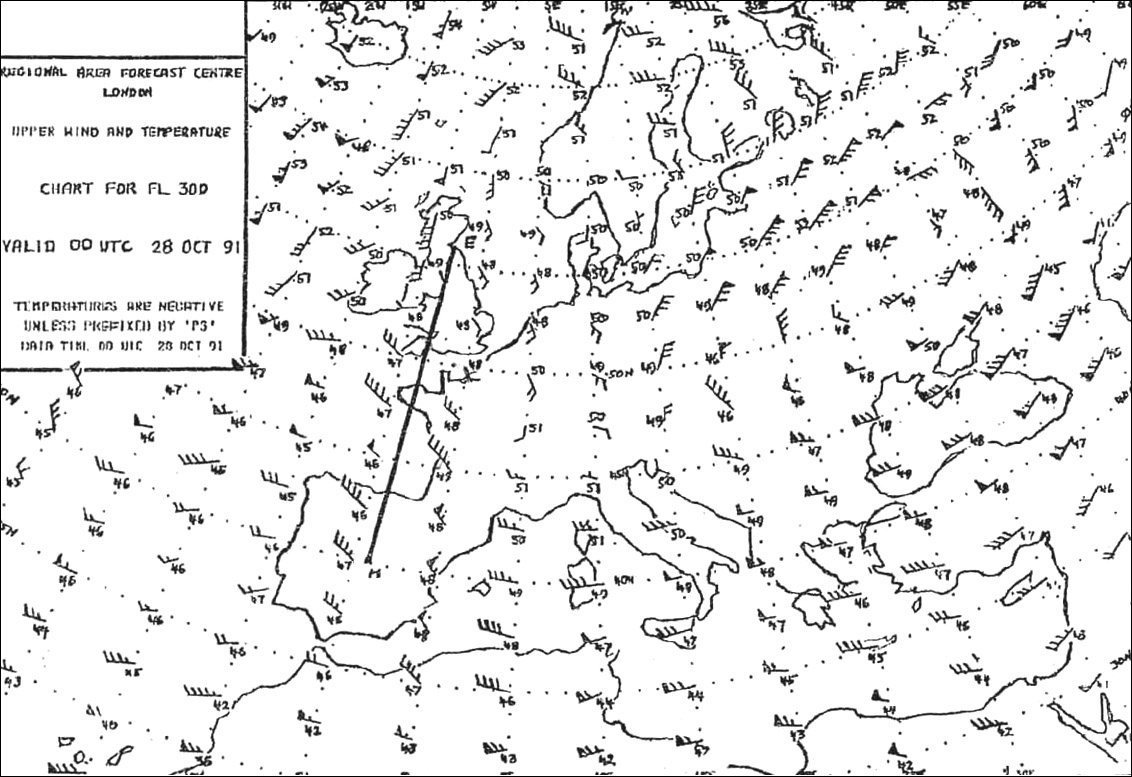exemple 339 1 et 2.1 et 2.

Quelle affirmation est vraie à propos d'un compas à lecture directe ?

Question 139-27 : Avant le décollage le compas à lecture directe devrait être vérifié en comparant l'information avec l'axe de la piste le compas à lecture directe est utilisable si l'indication durant le décollage ne diffère pas de plus de 2° par rapport à l'axe de piste vrai le compas à lecture directe est utilisable si l'indication durant le décollage ne diffère pas de plus de 2° par rapport à la route magnétique donnée sur la carte le cap du compas à lecture directe peut seulement être vérifié avec l'axe de piste après l'avoir corrigé de la déclinaison

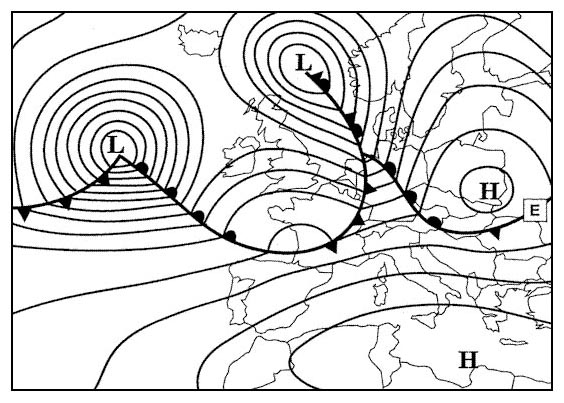exemple 343 Avant le décollage le compas à lecture directe devrait être vérifié en comparant l'information avec l'axe de la piste.Avant le décollage le compas à lecture directe devrait être vérifié en comparant l'information avec l'axe de la piste.

Près du pôle magnétique ?

Question 139-28 : La composante horizontale du champ magnétique terrestre est trop faible pour permettre d'utiliser un compas magnétique l'angle d'inclinaison est minimal et l'aiguille d'un compas à pivot sera presque verticale la composante verticale du champ magnétique terrestre est trop faible pour permettre d'utiliser un compas magnétique l'angle d'inclinaison est maximal et l'aiguille d'un compas à pivot sera presque horizontale

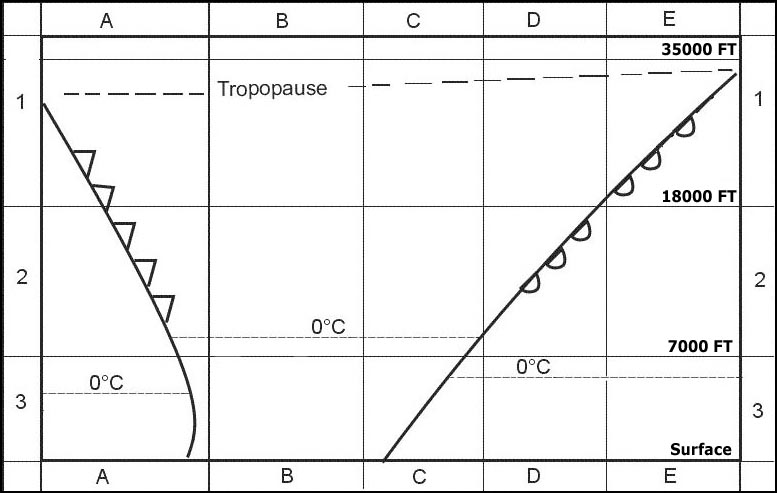exemple 347 La composante horizontale du champ magnétique terrestre est trop faible pour permettre d'utiliser un compas magnétique.La composante horizontale du champ magnétique terrestre est trop faible pour permettre d'utiliser un compas magnétique.

Selon la norme de certification cs 25 concernant le compas secours la ?

Question 139-29 : 10° 1° 5° 3°

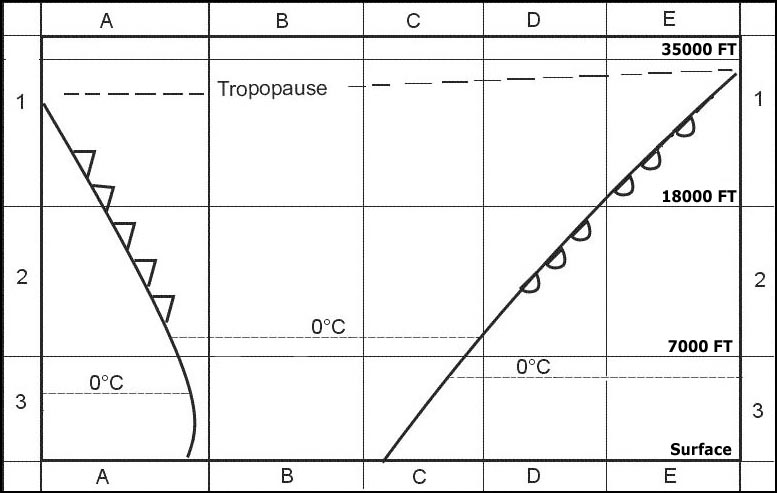exemple 351 10°.10°.

Pour cette question utiliser l'annexe ecqb 061 002 v2015 09 .la déviation au ?

Question 139-30 : 2° 2°e 2°w 0°

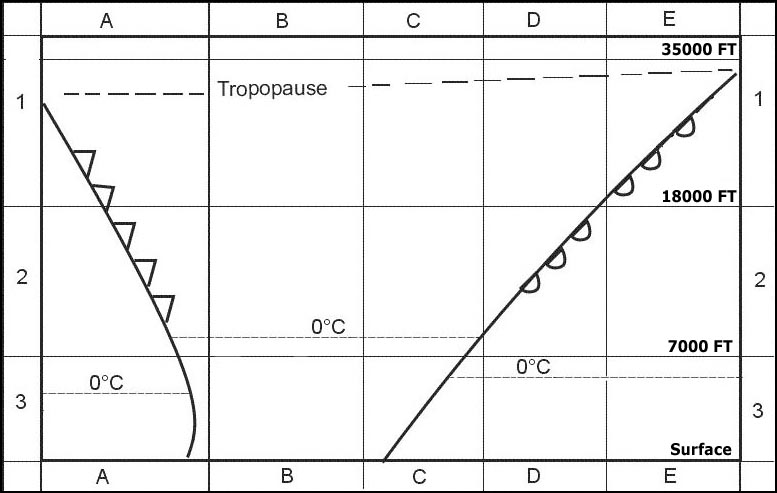Admin .la déviation est positive ou négative .la déviation est négative quand le nord du compas se trouve à gauche vers l'est du nord magnétique .la déviation est positive quand le nord du compas se trouve à droite vers l'ouest du nord magnétique exemple 355 -2°.-2°.

Un compas magnétique indique ?

Question 139-31 : Un cap compas une route magnétique un cap magnétique une route compas

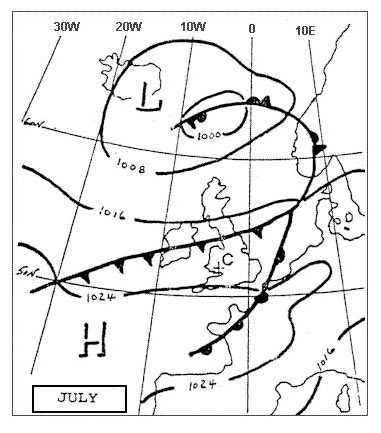exemple 359 Un cap compas.Un cap compas.

Le compas à lecture directe ?

Question 139-32 : Ne nécessite pas d'alimentation électrique par l'aéronef pour fournir une indication n'est pas sensible aux interférences des autres composants et systèmes de l'aéronef est certifié uniquement pour une utilisation en vfr et en vol pendant les horaires de jour publiés est plus fiable qu'un compas gyroscopique durant les virages et les accélérations ou les décélérations

exemple 363 Ne nécessite pas d'alimentation électrique par l'aéronef pour fournir une indication.Ne nécessite pas d'alimentation électrique par l'aéronef pour fournir une indication.

Votre compas magnétique indique un cap 090° 'e' .si la déviation est de 3° ?

Question 139-33 : 087° 093° 096° 090°

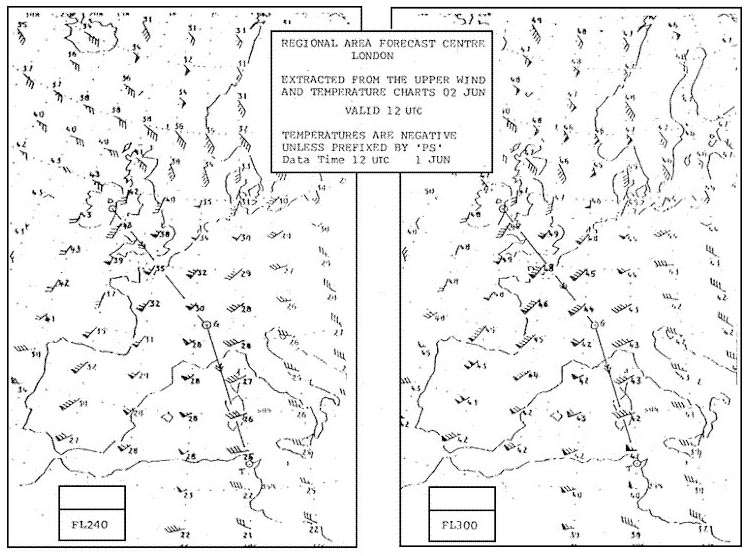exemple 367 087°.087°.

Un point a est situé sur l'équateur à une longitude de 130°00'e .le point b ?

Question 139-34 : 01°11's 128°49'e 01°11'n 131°11'e 01°11'n 128°49'e 01°11's 131°11'e

Admin .on part au sud et en direction de l'ouest donc c'est la seule réponse possible .par le calcul .01°11' = 60 + 11 = 71'.g = 71 x tan 45 angle entre le sud et la route = 71.gb = 130° 1°11' = 128° 49'.attention ici on trouve la valeur 1°11' identique à la latitude c'est parce qu'on se trouve à l'équateur sinon on doit déduire la longitude du lieu ou l'on se trouve .par exemple on est au départ à 01°s on déduit 71 60 = 11'.puis on applique >130° 11' = 129°49' exemple 371 01°11's 128°49'e01°11's 128°49'e

L'échelle nominale d'une carte de projection conique lambert est ?

Question 139-35 : L'échelle aux parallèles standards l'échelle moyenne entre le pôle et l'équateur l'échelle moyenne entre les parallèles du cône sécant l'échelle à l'équateur

Admin . 1776.sur une carte de projection conique lambert canevas lambert conique conforme l'échelle sur la carte est correcte sur les parallèles standards .l'échelle moyenne entre les parallèles du cône sécant est inférieure à l'échelle nominale aux parallèles standards exemple 375 L'échelle aux parallèles standards.L'échelle aux parallèles standards.

La carte généralement utilisée pour la navigation dans les zones polaires ?

Question 139-36 : Projection stéréographique projection mercator directe projection gnomonique projection lambert conforme

exemple 379 Projection stéréographique.Projection stéréographique.

L'échelle à l'équateur d'une carte mercator est 1 / 3 704 000 son échelle ?

Question 139-37 : 1 / 1 852 000 1 / 7 408 000 1 / 3 208 000 1 / 185 200

Admin .la question dit qu'à l'équateur 1 unité sur la carte vaut 3 704 000 unité en réalité .a la latitude 60° sud ou nord cela n'a pas d'importance 1 unité des mm par exemple ne représentera plus que 1 852 000 unité en réalité avec la formule et le calcul suivant .a la latitude 60° l'échelle est de 1/3 704 000 x 1/cos60° .Échelle = 1 / 3 704 000 x 1 / 0 5 .Échelle = 1 / 3 704 000 x 0 5 .Échelle = 1 / 1 852 000 exemple 383 1 / 1 852 0001 / 1 852 000

Les parallèles de référence d'une projection conique lambert sont les ?

Question 139-38 : 0 39 0 60 0 92 0 42

Admin .constante de cône .k = sin latitude moyenne ..07°40'n 38°20'n = 30°40'.30°40'/2 = 15°20'.07°40' + 15°20' = 23°n..constante de cône = sin 23 = 0 39 exemple 387 0,39.0,39.

Sur une carte de projection conique lambert la convergence des méridiens ?

Question 139-39 : Est la même que la convergence terrestre au parallèle de tangence est nulle pour l'ensemble de la carte varie comme la sécante de la latitude est égale à la convergence terrestre aux parallèles standards

Admin .retenez que sur une carte lambert l'échelle est correcte le long des parallèles standards et la convergence est correcte au parallèle d'origine là où le cône de la projection tangente la surface du globe .le cône de projection est soit défini tangent à l'ellipsoïde de référence en un point défini par un méridien de référence et un parallèle de référence soit sécant à l'ellipsoïde selon deux parallèles mais le résultat sur une carte de projection conique lambert est le même les angles sont conservés exemple 391 Est la même que la convergence terrestre au parallèle de tangence.Est la même que la convergence terrestre au parallèle de tangence.

Une ligne droite tracée sur une carte mesure 4 63 cm et représente 150 nm ?

Question 139-40 : 1 6 000 000 1 5 000 000 1 1 000 000 1 3 000 000

Admin .150 nm = 277 8 km = 27780000 cm.27780000 / 4 63 cm = 1/6000000 exemple 395 1 : 6 000 000.1 : 6 000 000.

~

Droits exclusifs réservés. Reproduction interdite sous peine de poursuites.

5519 Entrainement Examen gratuit